% matplotlib inline

import cv2
import numpy as np
import matplotlib.pyplot as plt
import seaborn

def histeq(img, num_gl):
    """Computes a histogram equalization transform of the input image.
    
    Args:
        img: MxN numpy array of int. Input image that is to be transformed.
        num_gl: int. Number of graylevels in input image.
        
    Returns:
        trans_img: MxN numpy array of int. Histogram equalized image.
    """

    N, M = img.shape

    norm_hist = np.array([np.sum(img == g) for g in range(num_gl)])/(N*M)
    cumul_hist = np.array([np.sum(norm_hist[:g+1]) for g in range(num_gl)])

    transform = np.round((num_gl - 1)*cumul_hist).astype(int)
    trans_img = transform[img]
    
    return trans_img, transform

img = np.array([[1, 1, 1, 4, 4, 4, 4, 3],
                [1, 1, 1, 2, 2, 3, 2, 2],
                [1, 1, 1, 4, 4, 2, 4, 0],
                [1, 1, 1, 2, 3, 3, 4, 0],
                [1, 1, 1, 2, 1, 4, 4, 3],
                [4, 1, 2, 1, 1, 1, 1, 1],
                [4, 4, 4, 1, 1, 1, 1, 1],
                [4, 2, 4, 3, 2, 4, 4, 0]])
trans_img, _ = histeq(img, 8)

print(trans_img)

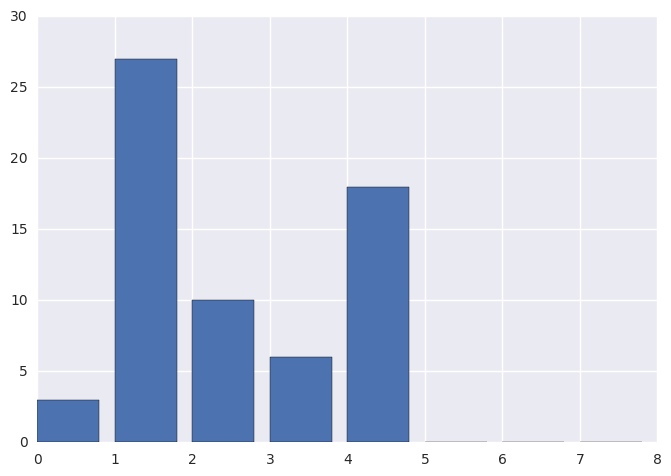
orig_hist, _ = np.histogram(img, bins=8, range=(0, 8))
print(orig_hist)
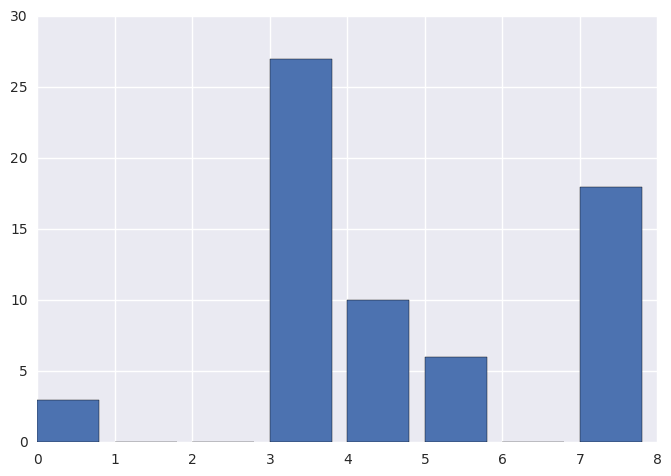
plt.bar(range(0, 8), orig_hist)

trans_hist, _ = np.histogram(trans_img, bins=8, range=(0, 8))
print(trans_hist)
plt.bar(range(0, 8), trans_hist)

# If you are going to compare this result to the one in the lecture slides,
# note that this image is not identical.
img = cv2.imread('../../assets/images/car.png', cv2.IMREAD_GRAYSCALE)
histeq_img, _ = histeq(img, 256)

plt.figure(0)
plt.imshow(img, cmap='gray')
plt.axis('off')
plt.figure(1)
plt.imshow(histeq_img, cmap='gray')
plt.axis('off')

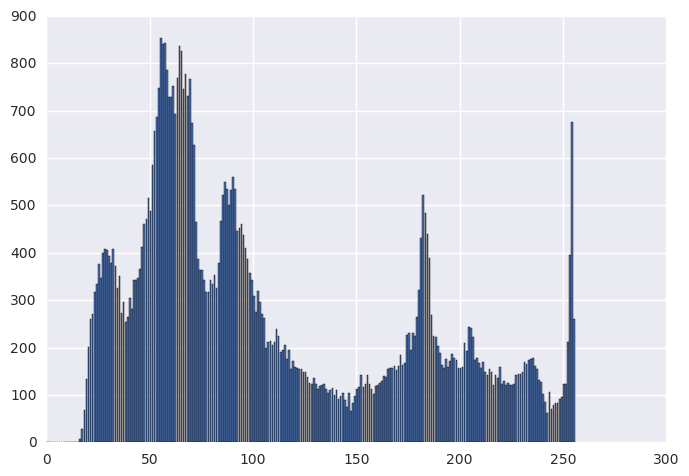
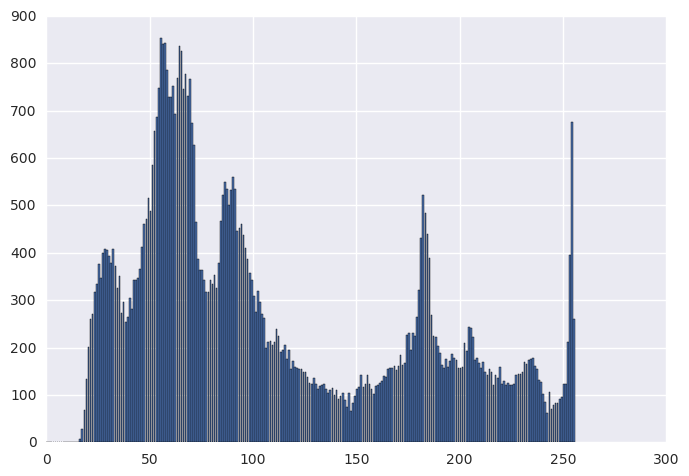
orig_hist, _ = np.histogram(img, bins=256, range=(0, 256))
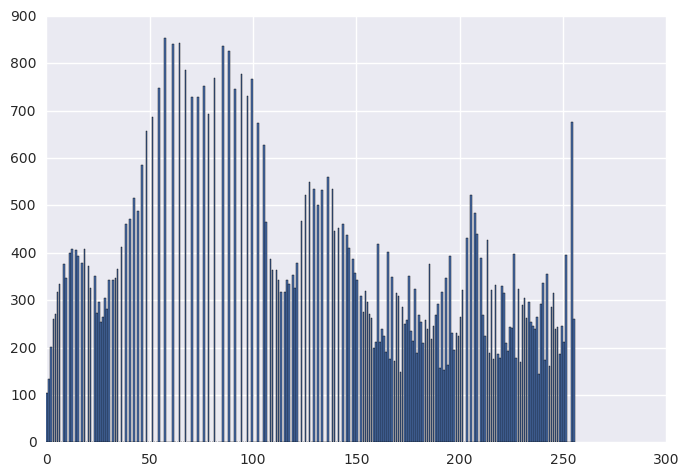
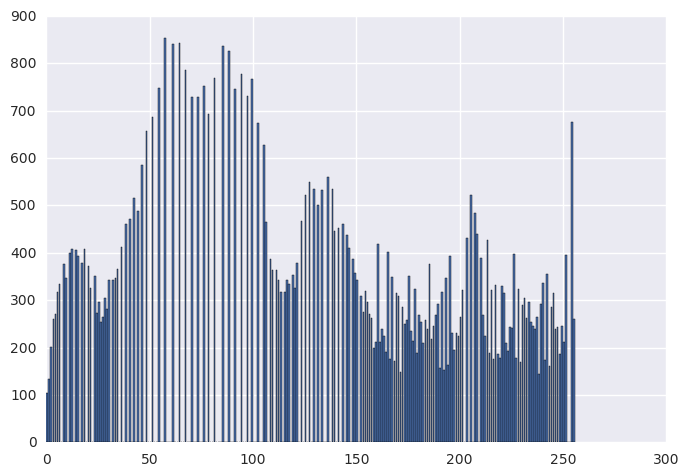
histeq_hist, _ = np.histogram(histeq_img, bins=256, range=(0, 256))

plt.figure(0)
plt.bar(range(0, 256), orig_hist)
plt.figure(1)
plt.bar(range(0, 256), histeq_hist)

def gaussian(x, mu, sigma):
    """Compute the Gaussian probability mass function (pmf) and cumulative mass function (cmf)
    
    Args:
        x: 1D numpy array
        mu: Mean value of distribution
        sigma: Standard deviation of distribution
        
    Returns:
        pmf: 1D numpy array of same size as x. Gaussian probability mass function.
        cmf: 1D numpy array of same size as x. Gaussian cumulative mass function.
    """
    
    # We do not compute the pmf
    #
    #   pmf = 1 / np.sqrt(2*np.pi*sigma**2)*np.exp(-(x - mu)**2 / (2*sigma**2))
    #
    # directly. Instead we compute the logarithm, and then take the exp of the logarithm.
    # This mitigates overflow errors (since the exponential tends to be quite large for
    # large arguments (when x is large)).
    log_pmf = -1/2*np.log(2*np.pi*sigma**2) - (x - mu)**2 / (2 * sigma**2)
    pmf = np.exp(log_pmf)
    cmf = np.array([np.sum(pmf[:i+1]*(x[1] - x[0])) for i, _ in enumerate(x)]) # NB step size is assumed uniform over x
    
    return pmf, cmf

# Let us test the implementation
from scipy.stats import norm

x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1

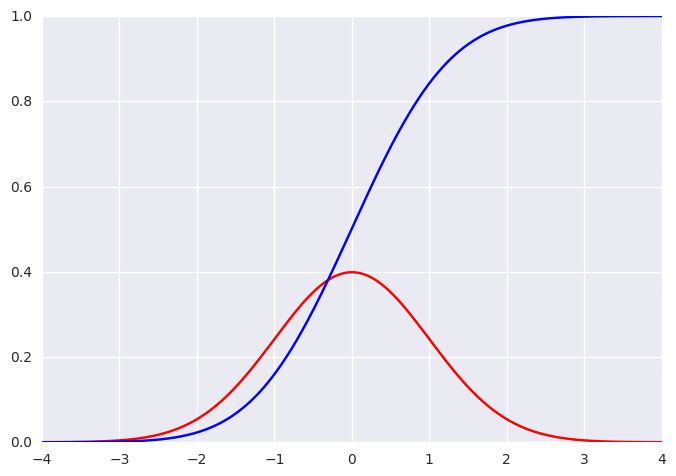
pmf, cmf = gaussian(x, mu, sigma)

plt.figure(0)
plt.plot(x, pmf, 'r')
plt.plot(x, cmf, 'b')

# Ensure that our implementation makes sense
print(np.linalg.norm(pmf - norm.pdf(x, mu, sigma)))
print(np.linalg.norm(cmf - norm.cdf(x, mu, sigma)))

def match_hist_to_gauss(img, num_gl, mu, sigma):
    """Performs a histogram matching on the input image.
    
    Args:
        img: MxN numpy array of int. Input image that is to be transformed.
        num_gl: int. Number of graylevels in input image.
        mu: float. Desired mean of the matched normal distribution.
        sigma: float. Desired standard deviation of the matched normal distribution.
        
    Returns:
        trans_img: MxN numpy array of int. Histogram transformed image.
    """
    
    # Get the histogram-equalized image, and the transform from the function we made above
    histeq_img, histeq_trans = histeq(img, num_gl)
    
    # Get the desired probability mass function and cumulative mass function
    # (in this case from the Gaussian distribution). It is rather important
    # that the length of the pmf and cmf is of size num_gl such that there
    # is one value for each graylevel
    x = np.linspace(0, num_gl-1, num_gl)
    norm_pmf, norm_cmf = gaussian(x, mu, sigma)
    
    # Create a new mapping from the histeq to the wanted image
    norm_map = np.round((num_gl - 1)*norm_cmf)
    inv_norm_map = np.array([int(np.argmin(np.abs(norm_map - histeq_trans[g]))) for g in range(num_gl)])
    
    # More verbose version of the list comprehension above (note that np.argmin returns the smallest
    # index if there are more than one):
    # inv_norm_map = np.zeros(num_gl)
    #for g in range(num_gl):
    #   closest_index = int(np.argmin(np.abs(norm_map - histeq_trans[g])))
    #   inv_norm_map[g] = closest_index
    
    # Create a new image based on this transform
    trans_img = inv_norm_map[histeq_img.astype(np.uint8)]
    trans_img = np.zeros_like(histeq_img)
    
    for ind, val in enumerate(histeq_trans):
        trans_img[histeq_img==val] = inv_norm_map[ind]
    
    # Scale it back to original value range (assumed here to be [0, 255])
    
    #return 255*(np.max(trans_img) - trans_img)/(np.max(trans_img) - np.min(trans_img))
    return trans_img

mu = 128
sigma = 30
num_gl = 256
norm_img = match_hist_to_gauss(img, num_gl, mu, sigma)

# Compare images
plt.figure(0)
plt.imshow(img, cmap='gray')
plt.axis('off')
plt.figure(1)
plt.imshow(histeq_img, cmap='gray')
plt.axis('off')
plt.figure(2)
plt.imshow(norm_img, cmap='gray')
plt.axis('off')

# Compare histograms
orig_hist, _ = np.histogram(img, bins=256, range=(0, 256))
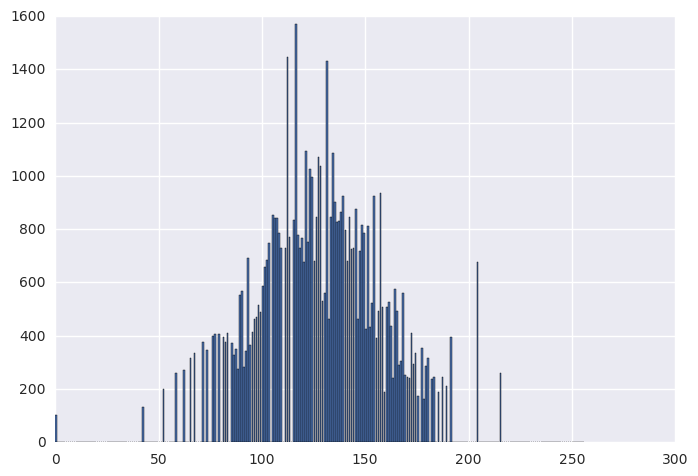
norm_hist, _ = np.histogram(norm_img, bins=256, range=(0, 256))

plt.figure(0)
plt.bar(range(0, 256), orig_hist)
plt.figure(1)
plt.bar(range(0, 256), histeq_hist)
plt.figure(2)
plt.bar(range(0, 256), norm_hist)