Solution proposal - week 13
Solutions to exercises week 13
INF2310, spring 2017
Task 1 - Shannon-Fano coding and Huffman coding
The Shannon-Fano partitions for this model is unique for a certain sorting of the symbols (in sorting the symbols, we can choose between placing “b” or “c” as the second most occuring symbol). If we use the sorting of the symbols that is given in the model and follow the suggestion on placing 0 to the left group and 1 to the right group, we get the following tree
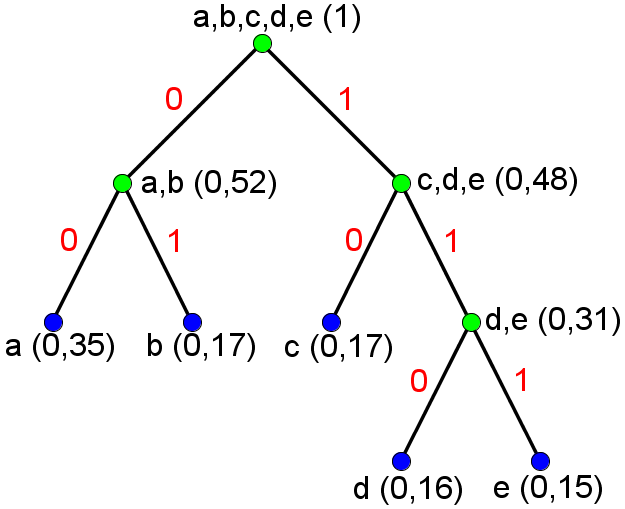
This gives rise to the following source code
| Symbol | Codeword |
|---|---|
| a | 00 |
| b | 01 |
| c | 10 |
| d | 110 |
| e | 111 |
The mean number of bits per symbol after the Shannon-Fano encoding is given as
where is the probability and is the length of the codeword corresponding to the symbol . In this case .
Let us assign 0 to the most probable group and 1 to the least probable group, and define that “b” shall be assigned 0 when it is joined with “c”. This results in the following tree
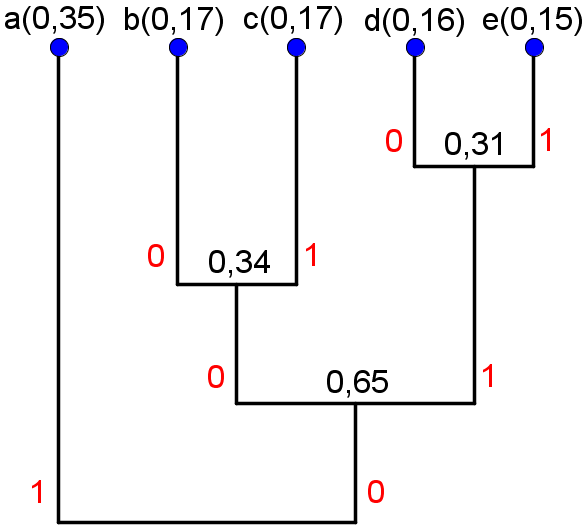
This gives rise to the following source code
| Symbol | Codeword |
|---|---|
| a | 1 |
| b | 000 |
| c | 001 |
| d | 010 |
| e | 011 |
The mean number of bits per symbols is . The symbol “a” is given a longer codeword with Shannon-Fano than with Huffman. Since the mean bits per symbol is lower for the Huffman than for Shannon-Fano, can we conclude that it is more space efficient to use a shorter codeword for “a”, even if the other codewords are as long or longer than in the Shannon-Fano coding.
Suggestion for a probability model
| Symbol | Probability |
|---|---|
| a | 0.42 |
| b | 0.15 |
| c | 0.15 |
| d | 0.14 |
| e | 0.14 |
None of the algorithms will behave differently when applied on this model. and .
Note: It seems like both the Shannon-Fano algorithm and the Huffman algorithm fits this model better, as the mean bits per symbol is low for both. It is worth considering the coding redundancy when studying how well a method suits a model. In the first model , and in the second . This means that the coding redundancy actually increases from model 1 to model 2 when using Shannon-Fano coding. Using Huffman coding, the coding redundancy decreases. In this sense, it seems like the Huffman code manages this new model better, and the Shannon-Fano code manages it worse. The reason why both achieve a reduction in can be attributed to the fact that the entropy is lower in this model, and thereby can achieve a (theoretical) better compression.
Task 2 - Huffman decoding
Follow the hint, and you will end up with the message Digital bildebehandling.
Task 3 - Huffman coding without coding redundancy
En Huffman-kode av meldingen “DIGITAL OVERALT!” er:
A Huffman encoding of the message DIGITAL OVERALT! is
| Symbol | Codeword | Occurances |
|---|---|---|
| ^ | 1000 |
1 |
| ! | 1101 |
1 |
| A | 000 |
2 |
| D | 1010 |
1 |
| E | 1111 |
1 |
| G | 1011 |
1 |
| I | 010 |
2 |
| L | 001 |
2 |
| O | 1001 |
1 |
| R | 1100 |
1 |
| T | 011 |
2 |
| V | 1110 |
1 |
We have 16 symbols in total, but only 12 unique, where the number of occurancies is either 1 or 2. This means that every probability can be written as a fraction where the numerator is 1 and the denominator is a power of 2 (8 or 16). That is, every symbol probability can be written as for . In this case (if $k$ is an integer), we know that Huffman coding will encode messages without coding redundancy, which means that the entropy is equal to the mean number of bits per symbol. We can therefore find the entropy in this message by computing the average number of bits per symbol after encoding, which is not involving any logarithms.
Task 4 - Huffman coding
Example of Huffman encoding implementation. Based on the implementation found at https://rosettacode.org/wiki/Huffman_coding#Python. This implementation uses the heap data structure to store the groups.
from heapq import heappush, heappop, heapify
from collections import defaultdict
def create_prob_model(message):
"""
Create an alphabeth based on the symbols in the message, and
attach a frequency to each symbol
"""
prob_model = defaultdict(int) # Every new key is given a default value of 0
for char in message:
prob_model[char] += 1 / len(message)
return prob_model
def huff_encode(message):
"""Huffman encoding of the input message.
Args:
message: String, a sequence of characters (symbols)
Returns:
source_code: Dict where every entry is {symbol: (frequency, codeword)}
encoded_message: String, bitstream of the encoded input message using the source_code.
"""
prob_model = create_prob_model(message)
heap = [[freq, [sym, ""]] for sym, freq in prob_model.items()]
heapify(heap)
while len(heap) > 1:
lo = heappop(heap)
hi = heappop(heap)
for pair in lo[1:]:
pair[1] = '0' + pair[1]
for pair in hi[1:]:
pair[1] = '1' + pair[1]
heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])
symbol_code_pairs = sorted(heappop(heap)[1:], key=lambda p: (len(p[-1]), p))
source_code = {}
for pair in symbol_code_pairs:
symbol = pair[0]
codeword = pair[1]
freq = prob_model[symbol]
source_code[symbol] = (freq, codeword)
encoded_message = ''
for symbol in message:
encoded_message += source_code[symbol][1]
return source_code, encoded_message
Example
message = "this is an example for huffman encoding"
source_code, encoded_message = huff_encode(message)
print("Message: {}".format(message))
print("Encoded message: {}\n".format(encoded_message))
print("Symbol Frequency Codeword")
for symbol, pair in sorted(source_code.items()):
print("{0:>6} {1:>9,.2f} {2:>8}".format(symbol, pair[0], pair[1]))
Message: this is an example for huffman encoding
Encoded message: 1000000011110011110111100111101100101010111001111010010010011000000111001011101001101101101000110001110111010010100101010111000101111100011111111111001000000
Symbol Frequency Codeword
0.15 101
a 0.08 1001
c 0.03 111110
d 0.03 111111
e 0.08 1100
f 0.08 1101
g 0.03 00000
h 0.05 0001
i 0.08 1110
l 0.03 00001
m 0.05 0010
n 0.10 010
o 0.05 0011
p 0.03 01100
r 0.03 01101
s 0.05 0111
t 0.03 10000
u 0.03 10001
x 0.03 11110
Task 5 - Arithmetic coding, Huffman coding and entropy
The symbols “a”, “b”, “c” and “d” have occurancies of 2, 1, 2, and 5, respectively. One valid approach for the Huffman encoding is therefore
- Join the groups and with a total number of occurances of 3.
- Join the groups and with a total number of occurances of 5.
- Join the groups and .
In the resulting Huffman source code, the length of the codewords will be 3, 3, 2, and 1 for the symbols “a”, “b”, “c”, and “d”, respectively, which means that the mean bps is 1.8. Starting with as current interval shall produce a final current interval at about .
The shortest possible binary representation of a number in this interval is
, which means that the encoded
message is 000111010110011.
Since there is 15 bits in the arithmetic code, and 10 symbols in the message, the mean bps will be 1.5 after the arithmetic encoding. The reason why arithmetic coding can achieve lower mean bps than the entropy bound, is that it can encode symbols as floating point numbers (not restricted to integers). But note that the expected number of bps is still bounded by the entropy.
Based on this, it is expected that the coding redundancy after arithmetic coding of the random permutations of the original message to be positive (on average). In a test of 1000 runs with random permutations, the average coding redundancy was about 0.39, varying from -0.26 to 0.54.
Task 6 - arithmetic coding
Various functions needed for arithmetic coding and decoding follows
Finding decimal interval
import numpy as np
def scale_interval_edges(orig_interval_edges, min_val, max_val):
"""Scale the original interval edges to the new min and max values"""
new_edges = min_val + (max_val - min_val)*orig_interval_edges
return new_edges
def symbol_to_index(symbol, alphabeth):
"""Map symbol to index according to alphabeth (1-based indexing since we are working on intervals,
the returned index will be according to the upper edge of the interval.)"""
assert len(set(alphabeth)) == len(alphabeth), 'Redundant alphabeth'
assert symbol in alphabeth, 'Symbol {} not in alphabeth'.format(symbol)
return alphabeth.index(symbol) + 1 #
def get_interval_from_symbol(current_symbol, alphabeth, current_min, current_max, orig_interval_edges):
"""Get a new interval for the new symbol, based on the current min and max and original interval edges"""
curr_signal_ind = symbol_to_index(current_symbol, alphabeth)
curr_interval_edges = scale_interval_edges(orig_interval_edges, current_min, current_max)
new_min = curr_interval_edges[curr_signal_ind - 1]
new_max = curr_interval_edges[curr_signal_ind]
return (new_min, new_max)
def interval_edges(pmf):
"""Return a list of interval edges, given the probability mass function"""
return np.array([np.sum(pmf[:i]) for i in range(len(pmf) + 1)])
def arithmetic_intervals(alphabeth, signal, pmf):
"""Get a list of intervals obtained by arithmetic coding of signal.
Args:
alphabeth: List of unique characters.
signal: String of symbols, where every symbol need to be a member of alphabeth.
pmf: Probability mass function for elements in alphabeth. The order follows
the order of alphabeth, that is pmf[i] is the probability of alphabeth[i].
Returns:
intervals: List of (min, max) float tuples, where (min, max) is the interval
edges of the respective symbol. This list has one interval per symbol in
the input signal.
"""
orig_interval_edges = interval_edges(pmf)
signal_list = list(signal)
curr_min, curr_max = get_interval_from_symbol(signal_list[0], alphabeth, 0.0, 1.0, orig_interval_edges)
intervals = [(curr_min, curr_max)]
for i, symbol in enumerate(signal_list[1:]):
curr_min, curr_max = get_interval_from_symbol(symbol, alphabeth, curr_min, curr_max, orig_interval_edges)
intervals.append((curr_min, curr_max))
return intervals
Decimal number to binary sequence
def binary_sequence(decimal):
"""Return a binary sequence representation of input.
Args:
decimal: scalar float in [0, 1) # Important that the interval is half-open
Returns:
bin_sequence: List of integers in {0, 1}
"""
reminder = decimal
bin_sequence = [int(np.floor(2*reminder))]
ind = 0
while reminder > 1e-10: # This is not very robust w.r.t. float precision
reminder = 2*reminder - bin_sequence[ind]
bin_sequence.append(int(np.floor(2*reminder)))
ind += 1
return bin_sequence
Find shortest binary representation within a decimal interval
def shortest_binary(d_interval):
"""Find shortest binary representation within a decimal interval.
Args:
d_interval: Tuple (d_min, d_max) of floats. This is a
half open interval [d_min, d_max) ⊆ [0, 1).
Returns:
bin_seq: Binary representation of shortest length within d_interval.
"""
d_min, d_max = d_interval
assert d_min < d_max, 'Need strictly increasing interval'
assert d_min >= 0, 'Negative lower bound on interval'
assert d_max < 1, 'Upper interval bound greater or equal to 1'
# Initialize current interval (c_min, c_max)
c_min = 0.0
c_max = 1.0
# We continue until the current interval (c_min, c_max) is contained inside
# the given interval (d_min, d_max).
# Note: Adding a 1 to the binary sequence increases c_min, but leaves c_max fixed.
# Adding a 0 to the binary sequence decreases c_max, but leaves c_min fixed.
k = 1
bin_seq = []
while True:
# Allways add 1 to bin_seq if possible
if c_min < d_min and c_min + 1/2**k < d_max:
c_min = c_min + 1/2**k
bin_seq.append(1)
else:
if c_max > d_max and c_max - 1/2**k > d_min:
c_max = c_max - 1/2**k
bin_seq.append(0)
else:
# No change is made to the current interval, we are finished
break
k = k + 1
return bin_seq
Encoding
def arithmetic_encoding(alphabeth, pmf, signal):
"""Encode a signal to a binary sequence.
Args:
alphabeth: List of unique characters.
signal: String of symbols, where every symbol need to be a member of alphabeth.
pmf: Probability mass function for elements in alphabeth. The order follows
the order of alphabeth, that is pmf[i] is the probability of alphabeth[i].
Returns:
bin_seq: Arithmetic encoding of input signal.
"""
intervals = arithmetic_intervals(alphabeth, signal, pmf)
bin_seq = shortest_binary(intervals[-1])
return bin_seq
Decoding
def interval_in_increasing(number, increasing_list):
"""Find the interval where number is located within the list of increasing numbers."""
assert number >= increasing_list[0], 'Number is outside increasing_list'
assert number <= increasing_list[-1], 'Number is outside increasing_list'
interval = None
for i in range(1, len(increasing_list)):
if number >= increasing_list[i-1] and number <= increasing_list[i]:
interval = (i-1, i)
assert interval is not None, 'Invalid input to interval_in_increasing'
return interval
def decimal_from_binary(bin_seq):
"""Every decimal number d_10 in [0, 1) can be represented as a power series
d_10 = b_1*1/2^1 + b_2*1/2^2 + b_3*1/2^3 + ...
where b_n are either 0 or 1.
Args:
bin_seq: [b_1, b_2, b_3, ...]
Returns:
decimal_num: The number that corresponds to the input bin_seq
"""
half_powered = np.array([1/2**k for k in range(1, len(bin_seq)+1)])
return np.dot(np.array(bin_seq), half_powered)
def arithmetic_decoding(alphabeth, pmf, encoded_signal, num_to_decode):
"""Decode binary signal to a signal with symbols from the alphabeth.
Args:
alphabeth: List of unique characters.
pmf: Probability mass function for elements in alphabeth. The order follows
the order of alphabeth, that is pmf[i] is the probability of alphabeth[i].
encoded_signal: List of 0 or 1.
num_to_decode: Number of symbols to decode.
Returns:
signal: String with symbols from alphabeth. The decoded signal.
"""
# Initial step
decimal_signal = decimal_from_binary(encoded_signal)
orig_interval_edges = interval_edges(pmf)
curr_symbol_inds = interval_in_increasing(decimal_signal, orig_interval_edges)
symbols = [alphabeth[curr_symbol_inds[0]]]
new_min = orig_interval_edges[curr_symbol_inds[0]]
new_max = orig_interval_edges[curr_symbol_inds[1]]
for num_decoded in range(1, num_to_decode):
curr_interval_edges = scale_interval_edges(orig_interval_edges, new_min, new_max)
curr_symbol_inds = interval_in_increasing(decimal_signal, curr_interval_edges)
symbols.append(alphabeth[curr_symbol_inds[0]])
new_min = curr_interval_edges[curr_symbol_inds[0]]
new_max = curr_interval_edges[curr_symbol_inds[1]]
return ''.join(symbols)
Examples
Define an alphabeth of symbols, and probabilities for each alphabeth. Then create a string of symbols from this alphabeth that you want to encode.
Test arithmetic_intervals() function
alphabeth = ['a', 'b', 'c']
pmf = np.array([0.6, 0.2, 0.2]) # Probability mass function for alphabeth (must sum to 1)
signal = 'abccba'
intervals = arithmetic_intervals(alphabeth, signal, pmf)
for interv in intervals:
print(interv[0], interv[1])
0.0 0.6
0.36 0.48
0.456 0.48
0.4752 0.48
0.47808 0.47904
0.47808 0.478656
Test the binary_sequence() function
print(binary_sequence(0.853515625))
[1, 1, 0, 1, 1, 0, 1, 0, 1, 0]
Test the shortest_binary() function
decimal_interval = (0.06752, 0.0688)
print(shortest_binary(decimal_interval))
[0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0]
Test entire encoding
encoded_signal = arithmetic_encoding(alphabeth, pmf, signal)
print(encoded_signal)
[0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0]
Test decoding
encoded_signal = [1, 0, 0, 0, 1]
decoded_signal = arithmetic_decoding(alphabeth, pmf, encoded_signal, 5)
print(decoded_signal)
acaba
Test encoding and decoding
alphabeth = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
pmf = np.array([8.167, 1.492, 2.782, 4.253, 12.702, 2.228, 2.015, 6.094, 6.966, 0.153, 0.772, 4.025, 2.406, 6.749, 7.507, 1.929, 0.095, 5.987, 6.327, 9.056, 2.758, 0.978, 2.360, 0.150, 1.974, 0.074]) / 100
signal = 'helloworld'
encoded_signal = arithmetic_encoding(alphabeth, pmf, signal)
decoded_signal = arithmetic_decoding(alphabeth, pmf, encoded_signal, len(signal))
print('Signal: {}'.format(signal))
print('Encoded signal: {}'.format(''.join([str(s) for s in encoded_signal])))
print('Decoded signal: {}'.format(decoded_signal))
Signal: helloworld
Encoded signal: 01011001101101000011111110010011011111010000
Decoded signal: helloworld