Exercise 4 - Shape representation

Task 1 (Problem 11.1 in Gonzales and Woods)

Show that redefining the starting point of a chain code so that the resulting sequence of numbers forms an integer of minimum magnitude makes the code independent of the initial starting point on the boundary.
Find the normalized starting point of the code 11076765543322.

Task 2 (Problem 11.8 in Gonzales and Woods)

Draw the medial axis of

A circle.
A square.
A rectangle.
An equilateral triangle.

Task 3 (Problem 11.9 in Gonzales and Woods)

For each of the figures shown.

Discuss the action taken at point $p$ by Step 1 of the skeletonizing algorithm presented in Section 11.1.7..
Repeat for Step 2 of the algorithm. Assume that p = 1 in all cases.

$\begin{array}{|c|c|c|} \hline 1 & 1 & 0 \\ \hline 1 & p & 0 \\ \hline 1 & 1 & 0 \\ \hline \end{array} \quad \begin{array}{|c|c|c|} \hline 0 & 0 & 0 \\ \hline 1 & p & 0 \\ \hline 0 & 0 & 0 \\ \hline \end{array} \quad \begin{array}{|c|c|c|} \hline 0 & 1 & 0 \\ \hline 1 & p & 1 \\ \hline 0 & 1 & 0 \\ \hline \end{array} \quad \begin{array}{|c|c|c|} \hline 1 & 1 & 0 \\ \hline 0 & p & 1 \\ \hline 0 & 0 & 0 \\ \hline \end{array}$

Task 4 - Create region objects using Python

In this practical exercise you will work your way through preprocessing, segmentation, creating region objects, and computing simple shape descriptiors.

Step 1: Get input image

Load the image tall_noise10_backgr.png. The image contains number on a noisy background. The background has both low frequent background variations and high frequent noise.

Figure 1: Image 'tall_noise10_backgr.png'.

Step 2: Remove hight-frequent noise

Try to filter out the high frequent noise using either a convolution low-pass filter or a median filter.

Step 3: Compute background

Thresholding the image using a global threshold does not work as the image has varying background. We can either compute the threshold in a local window, or estimate the background and subtract it from the image. Try estimating the background using either a mean filter or a median filter with a very large size (applied to the result from step 2). The filter size should be so large that the filtered image only shows the background, not the numbers.

Step 4: Remove the background

Compute the difference between the filtered image and the noise-filtered from point 2. Is the result you got now suitable for global thresholding? Experiment with filter sizes.

Step 5: Threshold the image using a global threshold.

Choose a suitable threshold value to separate the foreground from the background.

Step 6: Analyze the thresholded image

Analyze how good the thresholding is: are the numbers connected? Do we have one connected component per number? What about the frame?

Step 7: Compute region objects in python

Create a region label image to study how the regions correspond to numbers. Luckily, most imaging libraries have a built-in function to do this for us.

import cv2
# Compute thresholded_image from the steps above
connectivity = 4
output = cv2.connectedComponentsWithStats(thresholded_image,
                                          connectivity,
                                          cv2.CV_32S)
num_labels = output[0]
label_image = output[1] # Image with a unique label for each connected region
stats = output[2] 
centroids = output[3] # Centroid indices for each connected region
# stats is a num_labels x 5 array containing the following information about
# every connected component (component 0 is background).
# stats[0]: The leftmost coordinate which is the inclusive start of the
#           bounding box in the horizontal direction.
# stats[1]: The topmost coordinate which is the inclusive start of the
#           bounding box in the vertical direction.
# stats[2]: The horizontal size of the bounding box.
# stats[3]: The vertical size of the bounding box.
# stats[4]: The total area (in pixels) of the connected component.

Step 8: Investigate region properties

Use region and bounding box information to locate noise and frame regions. Use histogram and/or scatterplots in the investigation.

Step 9. Threshold the image based on the information you acquired.

# Hint on how to use the labeled image together with some conditions to
# segment out the labels not meeting said conditions . Here condition* are arrays of
# length num_labels, e.g. (region_area > threshold1) where region_area = stats[:, 4].

keep_labels = np.where(np.logical_and(condition1, condition2, condition3, ...))
keep_label_image = np.in1d(label_image, keep_labels).reshape(label_image.shape)
some_image[keep_label_image] = 255
some_image[keep_label_image == False] = 0

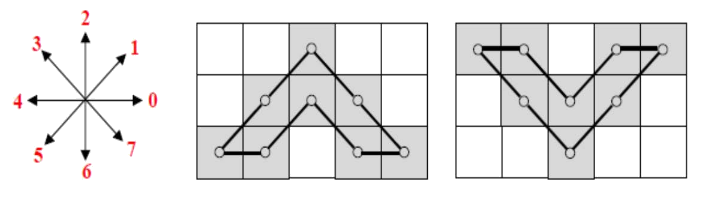
Task 5 - Exercise 1 from 2011 exam: chain codes

You are given the 8-directional chain code and the two objects below.

Chain code the boundary of the $\Lambda$ -shaped object clockwise from the lower left pixel.
Which technique, based on the 8-directional absolute chain code, can be used to make a description of the $\Lambda$ -shaped object that is independent of the start point? Demonstrate this by starting at the top pixel of the object, instead of the lower left.
The V-shaped object is a rotation of the $\Lambda$ -shaped object. Which technique, based on the clockwise relative chain code, will give you the same description of the two objects, independent of the start point? Demonstrate this by starting at the upper left pixel of the V-shaped object.

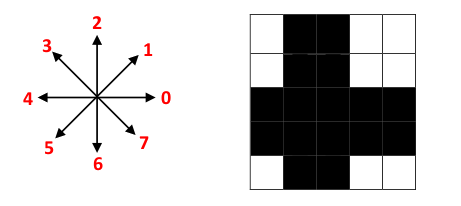
Figure 2: 8-directional chain code and two objects.

Task 6 - Exercise 1 from 2012 exam: chain codes

You are given the 8-directional chain code and the object below, where black is object pixels.

Chain code the boundary of the object clockwise from the upper left pixel.
Which technique will make the code invariant to the choise of start point? Demonstrate this by starting at the lower right pixel of the object.
Which technique will make the code rotation invariant? Demonstrate this by rotating the object $\pi / 2$ counterclockwise and start at one of the same object pixels as above.

Figure 3: 8-directional chain code and one object.