Task 1

Python exercise for classification based on a multivariate Gaussian classifier.

Step 1: Implement a Gaussian classifier using a d-dimensional feature vector

For the algorithm, see lecture slides or the notes.

It is recommended that you use the built-in functions for computing matrix inverse, determinant, means and covariance matrices, but you should implement the rest of the algorithm yourself.

import numpy as np

# Matrix determinant and inverse
A = np.array([[1, 2, 3], [2, 2, 6], [3, 6, 1]])
det_A = np.linalg.det(A)
# Check if A is invertible
if det_A != 0:
  A_inv = np.linalg.inv(A)

# Mean and covariance
## From matrix
B = np.array([[1, 2, 3], [4, 6, 8]])
cov_B = np.cov(B)
col_mean = np.mean(B, axis=0)
row_mean = np.mean(B, axis=1)

## From vectors
c = np.array([1, 2, 3])
d = np.array([4, 6, 8])
cov_cd = np.cov(c, d)
mean_c = np.mean(c)
mean_d = np.mean(d)

## Check for equality
assert (cov_B == cov_cd).all(), "Unequal covariance"
assert (col_mean == np.mean(np.stack([c, d]), axis=0)).all(), "Unequal column mean"
assert (row_mean == np.stack([mean_c, mean_d])).all(), "Unequal row mean"

Step 2: Train the classifier

Train the classifier using the mask tm_train.png (found here) to estimate the class-specific mean vector and covariance matrix.

If you want to verify that your code gives the correct classification labels, check the resulting classification image you get when you classify the entire image (all 6 wavelength bands tm1.png, …, tm6.png), against the result tm_classres.mat (which can be found here). In this image, each pixel is assigned a class label in $\{1, 2, 3, 4\}$.

You can find the test result as a grayscale image tm_classres.png in the image folder, but if you want to read the .mat file directly in python, here is how you do it:

import scipy.io

classres_container = scipy.io.loadmat('/path/to/tm_classres.mat')
print(classres_container.keys()) # For info about what the .mat file contains
classres_image = classres_container['klassim']

# Check your result using the classified image "my_classified_image"
num_equal = np.sum(1*(my_classified_image == classres_image))

Step 3: Find the best feature for classification using single features

Run the classification on the multivariate (6-band) input image. Compute the percentage of correctly classified pixels when using all features, and compare it to using single features. The classification accuracy should be computed on the whole image using the test mask tm_test.png.

Also try the simplyfied covariance matrix $\Sigma = \sigma^2 I$. Which version gives the highest classification accuracy?

Task 2 - Finding the decision functions for a minimum distance classifier

A classifier that uses diagonal covariance matrices is often called a minimum distance classifier, because a pattern is classified to the class that is closest when distance is computed using Euclidean distance.

Figure 2.1 Fisher's Iris flower data set.

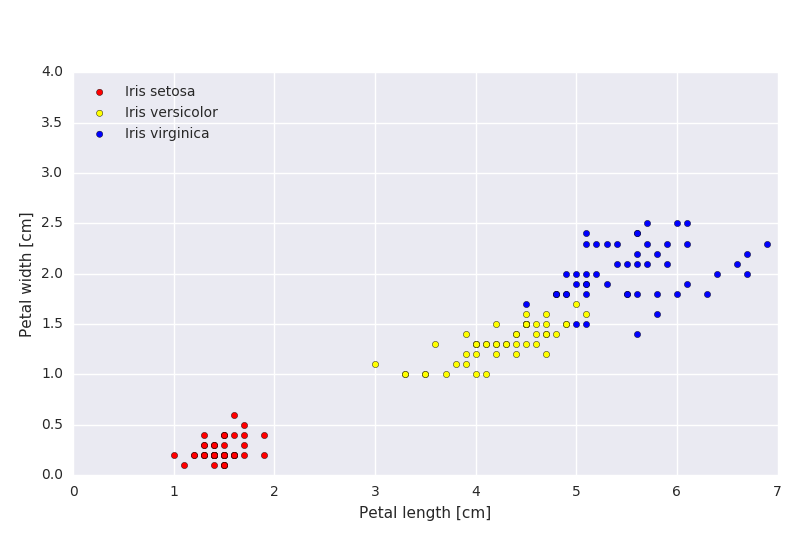
a)

In Figure 2.1, find the class means just by looking at the figure.

b)

If the data is classified using a minimum distance classifier, sketch the decision boundaries on the plot.

Task 3 - Discriminant functions

A classifier that uses Euclidean distance, computes the distance from a point $x$ to class $c$ as

Show that classification with this rule is equivalent to using the discriminant function

Task 4

In a three-class two-dimensional problem, the feature vectors in each class are normally distributed with covariance matrix

The mean vectors for the three classes are

Assuming that the classes are equally probable (the class prior is uniform):

a)

Classify the feature vector

according to a Bayesian classifier with the given covariance matrix.

b)

Draw the curves of equal Mahalanobis distance from the class with mean

Task 5

Given a two-class classification problem with equal class prior distribution

and Gaussian likelihoods

with means

and covariance matrix

Classify the feature vector

using Bayesian classification.