Solution proposal - exercise 8
Support Vector Machines
INF4300 - Digital Image Analysis
Ole-Johan Skrede
University of Oslo
October 2017
Task 1
Note: This is a somewhat elaborate explanation, but you will find the answer to Task 1 in it somewhere.
We introduce the Support Vector Machines with a binary, linearly separable classification problem. Let be a -dimensional feature vector, and the label of the class which belongs to. In the case of a binary classification, we have a training set
consisting of examples from two classes: and . (Notice that I use the more general “label 0” and “label 1” in stead of the labels which I find a bit limiting and confusing.) To make things easier below, we define the index sets , and .
We know that the data points (the feature vectors ) are linearly separable, which means that there exist (infinite) hyperplanes on the form
such that and .
We are going to write this last result on a particular form. In order to illustrate it, we use the 2D example shown in Figure 1.
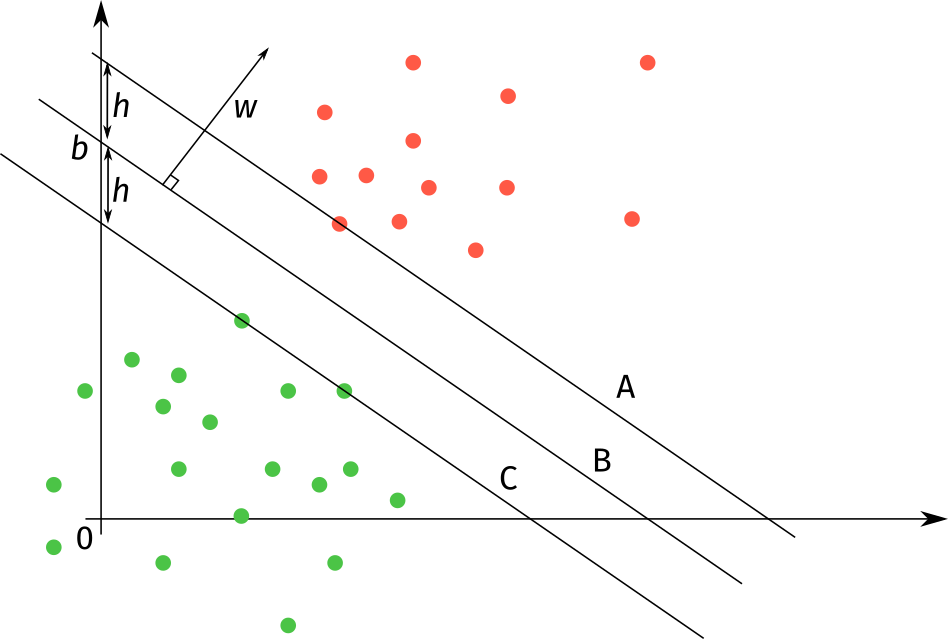
In this example, all red datapoints belong to class 0 and all green datapoints belong to class 1. We have drawn in 3 line segments.
- A: The line segment “closest” to class 0 such that all elements in class 0 are above it, and all elements in class 1 are below it.
- C: The line segment “closest” to class 1 such that all elements in class 1 are below it, and all elements in class 0 are above it. It also has the same slope (governed by as the line segment A.
- B: The line segment with slope that lies in the middle of A and C.
If you study the figure, you will notice that
or
If we scale the equations in the set with and respectively, we end up with
By introducing some indicator variables
and multiplying them into the equations above, we get
Updating and , we end up with the equation
This illustrates that we have some freedom to vary and within the constraints of the last equation.
Task 2
First, let us define the data
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
X_0 = np.array([[1, 9], [5, 5], [1, 1]])
X_1 = np.array([[8, 5], [13, 1], [13, 9]])
# Concatenate them and provide an extra label vector
X = np.vstack((X_0, X_1))
Y = np.array([0, 0, 0, 1, 1, 1])
Then, we create a scatter plot function that will be used throughout this exercise.
def make_meshgrid(X, h=.02, x_range=None, y_range=None):
"""Make a meshgrid covering the range of X. This is used to display classification regions.
Args:
X: numpy array of shape [n, 2] containing n 2d feature vectors
h: parameter controlling the resolution of the
"""
if x_range is None:
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
else:
x_min, x_max = x_range
if y_range is None:
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
else:
y_min, y_max = y_range
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
def scatter(X, Y, xx=None, yy=None, Z=None, plot_mean=False, x_range=None, y_range=None):
"""
Scatter plot with optional classification area and mean plot
Args:
X: numpy array of shape [n, 2] where n is the total number of datapoints
Y: numpy array of shape [n] containing the labels {1, 2, 3, ...} of X
xx: meshgrid x
yy: meshgrid y
Z: The result of applying some prediction function on all points in xx and yy
"""
#import seaborn as sns
#current_palette = sns.color_palette("muted", n_colors=5)
#cmap = ListedColormap(sns.color_palette(current_palette).as_hex())
cmap=plt.cm.coolwarm
if x_range is None:
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
else:
x_min, x_max = x_range
if y_range is None:
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
else:
y_min, y_max = y_range
plt.figure(figsize=(10, 10))
if xx is not None and yy is not None and Z is not None:
# Color class regions
plt.gca().contourf(xx, yy, Z, cmap=cmap, alpha=0.7)
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=cmap, marker='o', edgecolors='k')
if plot_mean:
mean_0 = np.mean(X[Y == 0], axis=0)
mean_1 = np.mean(X[Y == 1], axis=0)
plt.scatter(mean_0[0], mean_0[1], c='cyan', cmap=cmap, marker='x')
plt.scatter(mean_1[0], mean_1[1], c='magenta', cmap=cmap, marker='x')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.axes().set_aspect('equal')
plt.show()
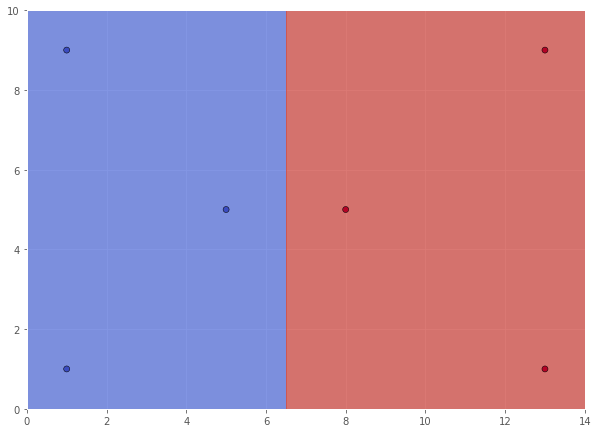
In this case, the decision boundary will be the vertical line segment at $x = 6.5.$ The support vectors will be the data points closest to the decision boundary, namely $(5, 5)$ for Class 0 and $(8, 5)$ for Class 1.
# Create a meshgrid of our domain
xx, yy = make_meshgrid(X)
# Define our class regions according to the decision boundary above
Z = (xx > 6.5)*1.0
scatter(X, Y, xx, yy, Z)
Task 3
a)
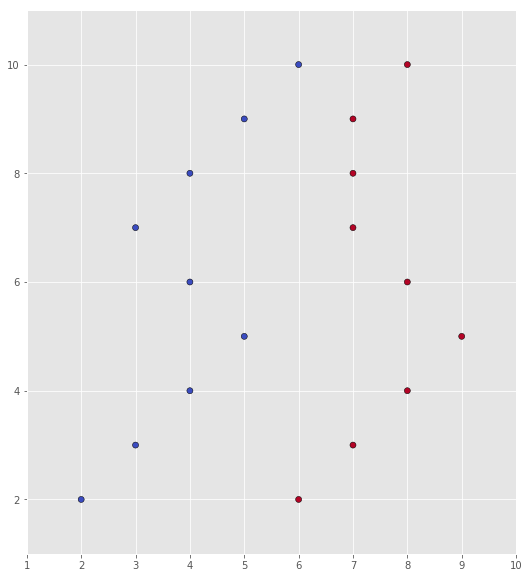
X = np.array([[2, 2], [3, 3], [4, 4], [5, 5], [4, 6], [3, 7], [4, 8], [5, 9], [6, 10],
[6, 2], [7, 3], [8, 4], [9, 5], [8, 6], [7, 7], [7, 8], [7, 9], [8, 10]])
Y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1])
scatter(X, Y)
b)
In the case of a Gaussian classifier with a scalar identity covariance matrix, the decision boundary (assuming equal priors) would be the line equidistant to the two class means, and normal on the line segment joining the two means. So, let us create a function that compute this line segment.
def compute_normal(X, Y):
"""
Computes the line consisting of points equidistant from the means
of data_0 and data_1.
A line (x, y) through a point (x0, y0) and normal to the line given by
the vector v = [a, b] will obey the following equation
a(x - x0) + b(y - y0) = 0.
In this case, the vector between the mean points is our normal vector,
and the point it should pass through is the average between the means.
"""
X_0 = X[Y == 0]
X_1 = X[Y == 1]
mean_0 = np.mean(X_0, axis=0)
mean_1 = np.mean(X_1, axis=0)
avg_01 = [(mean_0[0] + mean_1[0])/2, (mean_0[1] + mean_1[1])/2]
# Compute min and max for x, mostly for plotting reasons
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# Compute the line equidistant to both means
if mean_0[1] == mean_0[1]: # Vertical decision boundary
x = [avg_01[0] for _ in range(y_min, y_max)]
y = [i for i in range(y_min, y_max)]
else:
x = np.linspace(x_min, x_max)
y = avg_01[1] - (mean_1[0] - mean_0[0])/(mean_1[1] - mean_0[1])*(x - avg_01[0])
return np.column_stack((x, y))
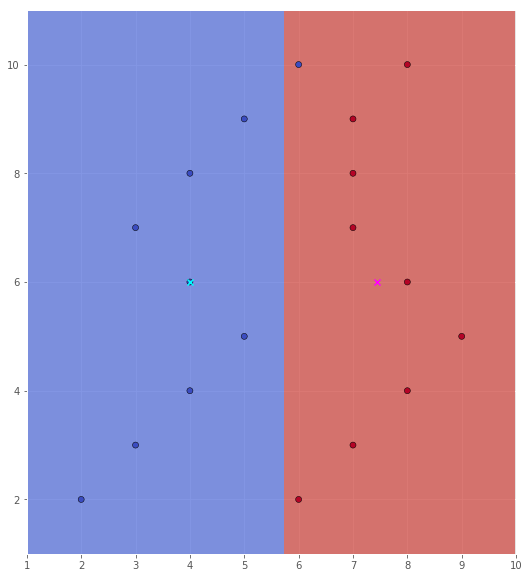
Now, we can use this function to plot the mean values together with the decision boundary.
decision_boundary = compute_normal(X, Y)
# In this case, the decision boundary happens to also be vertical
xx, yy = make_meshgrid(X)
Z = (xx > decision_boundary[0, 0])*1.0
scatter(X, Y, xx, yy, Z, plot_mean=True)
c)
We see that we classify one datapoint from Class 1 as Class 2, and since we have 18 data points in total, this would be an error rate of $1 / 18$ or about $5.6\%$.
d)
In this case, we can see (by inspection of the scatter plot) that the support vectors are $(5, 5)$, $(6, 10)$, $(7, 9)$. In order to draw the classification area, I use the svm module from the sklearn library. We will explore this library further below, so no explanation is given here.
from sklearn import svm
classifier = svm.SVC(C=100.0, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
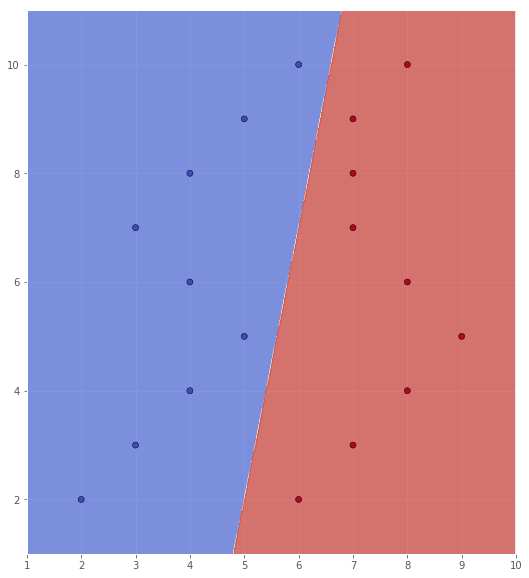
e)
As we can see, the SVM classifies the training set with an error rate of 0.
Task 4
Assuming that we have downloaded the data and put it in a reasonable location, we can take a look at it.
a)
## Load the data
import scipy.io
normaldistdata = scipy.io.loadmat('../../images/mynormaldistdataset.mat')
print("Normaldistdata keys: ", normaldistdata.keys())
bananadata = scipy.io.loadmat('../../images/mybananadataset.mat')
print("Bananadata keys: ", bananadata.keys())
Normaldistdata keys: dict_keys(['A', '__version__', '__header__', '__globals__', 'a'])
Bananadata keys: dict_keys(['__version__', 'A', 'B', 'a', '__header__', '__globals__', 'b'])
In this case, A contains data points and a contains corresponding labels. Similarly, b contains the labels for the data in B.
First, let us look at the data in normaldistdata.
X = normaldistdata['A']
Y = np.squeeze(normaldistdata['a'])
print("Number of datapoints in class 0: ", len(X[Y == 0]))
print("Number of datapoints in class 1: ", len(X[Y == 1]))
scatter(X, Y)
Number of datapoints in class 0: 100
Number of datapoints in class 1: 100
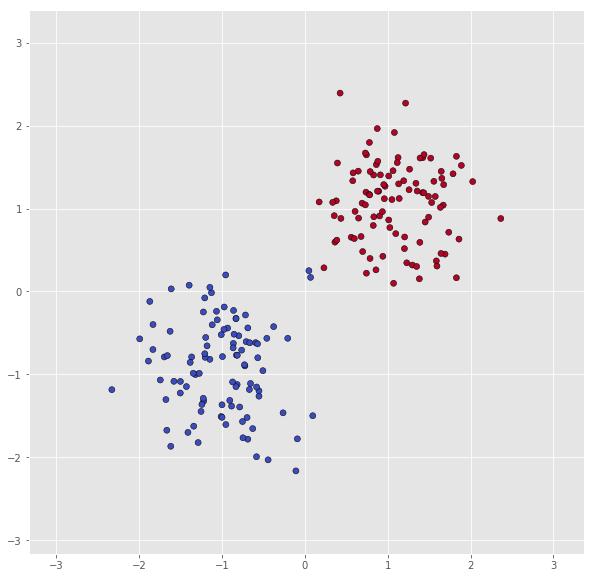
Then, dataset A in mybananadataset
X = bananadata['A']
Y = np.squeeze(bananadata['a'])
print("Number of datapoints in class 0: ", len(X[Y == 0]))
print("Number of datapoints in class 1: ", len(X[Y == 1]))
scatter(X, Y)
Number of datapoints in class 0: 94
Number of datapoints in class 1: 106
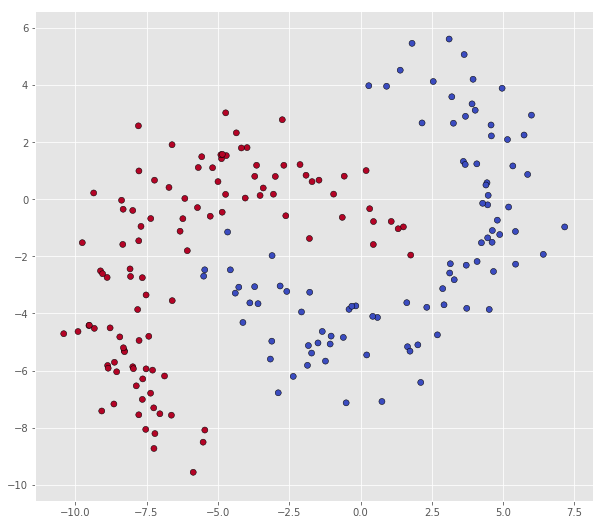
And finally, dataset B in mybananadataset
X = bananadata['B']
Y = np.squeeze(bananadata['b'])
print("Number of datapoints in class 0: ", len(X[Y == 0]))
print("Number of datapoints in class 1: ", len(X[Y == 1]))
scatter(X, Y)
Number of datapoints in class 0: 94
Number of datapoints in class 1: 106
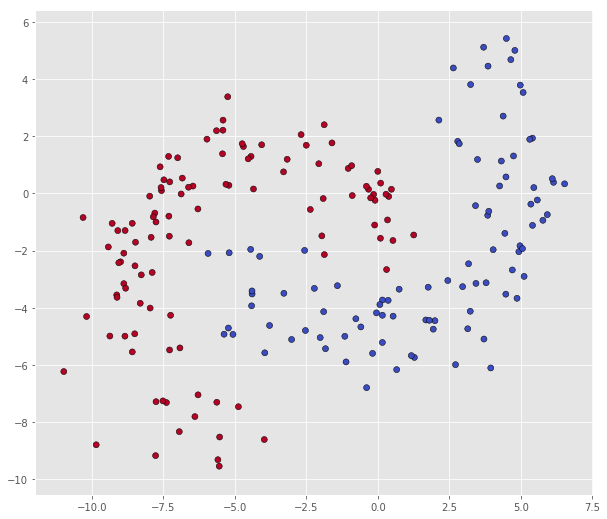
b)
First, we create some functions that we can use to evaluate the results
from collections import defaultdict
def evaluate(reference, proposal):
"""Compute evaluation metrics based on the confusion matrix of the proposed labeling,
given a reference labeling.
Confusion matrix relative to class 1:
PROPOSAL
class 0 1
REFERENCE 0 TN FP
1 FN TP
Note that in a multilabel (> 2) case, it would be useful to compute a metric for each label. In the binary
case, we can do it simpler by just naming label 1 as positive and label 0 as negative, and get one
value for each metric.
"""
num_classes = 2
cm = np.zeros((num_classes, num_classes))
for i, ref_val in enumerate(reference):
prop_val = proposal[i]
cm[ref_val, prop_val] += 1
metrics = defaultdict(list)
for c in range(num_classes):
metrics['TP'].append(cm[c, c]) # True positive
metrics['FP'].append(np.sum(cm[:, c]) - metrics['TP'][c]) # False positive
metrics['FN'].append(np.sum(cm[c, :]) - metrics['TP'][c]) # False negative
metrics['TN'].append(np.sum(cm) - metrics['TP'][c] - metrics['FN'][c] - metrics['FP'][c]) # True negative
# Sensitivity
if metrics['FN'][c] + metrics['TP'][c] > 0:
metrics['tpr'].append(metrics['TP'][c] / (metrics['FN'][c] + metrics['TP'][c]))
else:
metrics['tpr'].append(0.0)
# Specificity
if metrics['FP'][c] + metrics['TN'][c] > 0:
metrics['tnr'].append(metrics['TN'][c] / (metrics['FP'][c] + metrics['TN'][c]))
else:
metrics['tnr'].append(0.0)
# Precision
if metrics['FP'][c] + metrics['TP'][c] > 0:
metrics['ppv'].append(metrics['TP'][c] / (metrics['FP'][c] + metrics['TP'][c]))
else:
metrics['ppv'].append(0.0)
# Accuracy
if np.sum(cm) > 0:
metrics['acc'].append((metrics['TP'][c] + metrics['TN'][c]) / np.sum(cm))
else:
metrics['acc'].append(0.0)
return metrics
def average_metrics(list_of_metrics):
"""Average list of metrics."""
sum_metrics = {}
for metrics in list_of_metrics:
for key, metric in metrics.items():
if key in sum_metrics.keys():
sum_metrics[key] += np.array(metric)
else:
sum_metrics[key] = np.array(metric)
avg_metrics = {}
for key, val in sum_metrics.items():
avg_metrics[key] = val / len(list_of_metrics)
return avg_metrics
def pretty_print(metrics):
"""Print metrics in a table"""
print_header = True
for name, values in sorted(metrics.items()):
if print_header:
printstr = "{0:<20} ".format("Metric name")
for i, _ in enumerate(values):
printstr += "Label {0:<2} ".format(i)
printstr += "Average"
print_header = False
print(printstr)
printstr = "{0:<20} ".format(name)
for val in values:
printstr += "{0:>8,.3f} ".format(val)
printstr += "{0:>8,.3f}".format(np.mean(values))
print(printstr)
Now, we can start to explore the svm module.
from sklearn import svm
X = normaldistdata['A']
Y = np.squeeze(normaldistdata['a'])
classifier = svm.SVC()
classifier.fit(X, Y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
The model is now trained on the data, with the default hyperparameter values listed above. We can use this to classify new data points.
print("Point (1, 2) is predicted to have label", classifier.predict([[1, 2]]))
Point (1, 2) is predicted to have label [1]
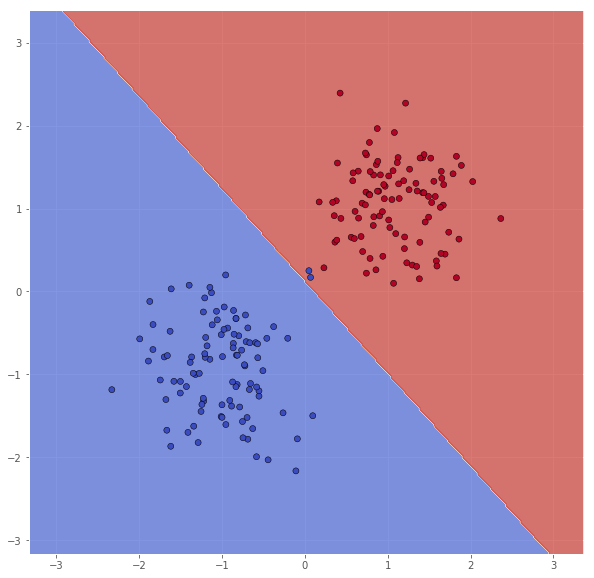
The parameters we care about in this task are C, kernel, and gamma. In this subtask we shall use a linear kernel, and various values of $C$. Let us try with $C = 1$ first.
classifier = svm.SVC(C=1.0, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 2.000 0.000 1.000
FP 0.000 2.000 1.000
TN 100.000 98.000 99.000
TP 98.000 100.000 99.000
acc 0.990 0.990 0.990
ppv 1.000 0.980 0.990
tnr 1.000 0.980 0.990
tpr 0.980 1.000 0.990
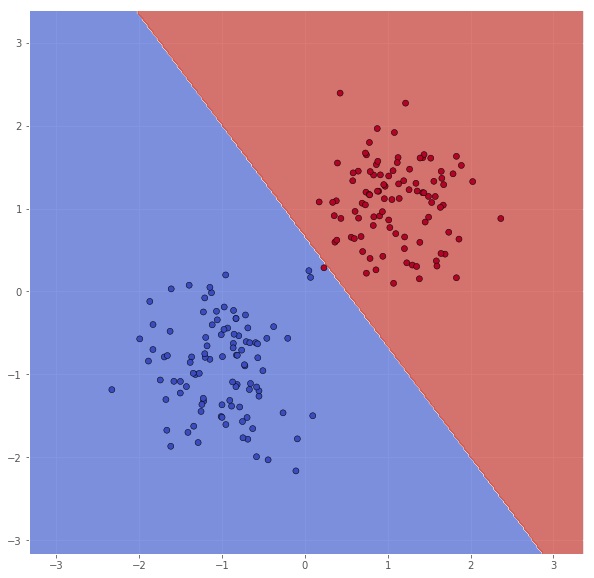
It seems like some of the outliers are missclassified. By increasing $C$, we can enforce stricter regularization, and try to leviate this.
classifier = svm.SVC(C=10.0, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 0.000 1.000 0.500
FP 1.000 0.000 0.500
TN 99.000 100.000 99.500
TP 100.000 99.000 99.500
acc 0.995 0.995 0.995
ppv 0.990 1.000 0.995
tnr 0.990 1.000 0.995
tpr 1.000 0.990 0.995
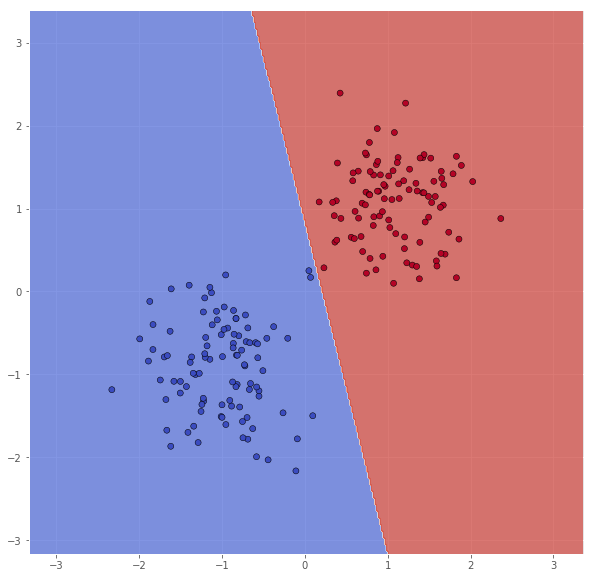
This is better, but it still seems like some of the outliers, now from the other class, are missclassified. We will try to increase $C$ once more.
classifier = svm.SVC(C=100.0, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 0.000 0.000 0.000
FP 0.000 0.000 0.000
TN 100.000 100.000 100.000
TP 100.000 100.000 100.000
acc 1.000 1.000 1.000
ppv 1.000 1.000 1.000
tnr 1.000 1.000 1.000
tpr 1.000 1.000 1.000
We now are able to classify the training set perfectly.
c)
The classifier also gives information about the support vectors.
print("Support vectors: ", classifier.support_vectors_)
print("Support vector indices: ", classifier.support_)
print("Number of support vectors for class 0 and class respectively: ", classifier.n_support_)
Support vectors: [[ 0.07008741 0.16943029]
[ 0.05 0.25 ]
[ 0.2316275 0.28493687]]
Support vector indices: [114 199 39]
Number of support vectors for class 0 and class respectively: [2 1]
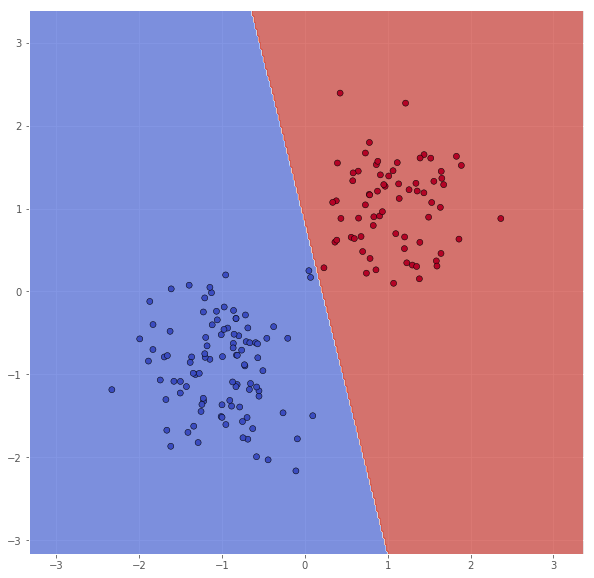
So, we can try to remove some vectors which indices are not [114, 199, 39].
X_sub = X[30:, :]
Y_sub = Y[30:]
classifier = svm.SVC(C=100.0, kernel='linear')
classifier.fit(X_sub, Y_sub)
xx, yy = make_meshgrid(X_sub)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X_sub, Y_sub, xx, yy, Z)
pretty_print(evaluate(Y_sub, classifier.predict(X_sub)))
Metric name Label 0 Label 1 Average
FN 0.000 0.000 0.000
FP 0.000 0.000 0.000
TN 70.000 100.000 85.000
TP 100.000 70.000 85.000
acc 1.000 1.000 1.000
ppv 1.000 1.000 1.000
tnr 1.000 1.000 1.000
tpr 1.000 1.000 1.000
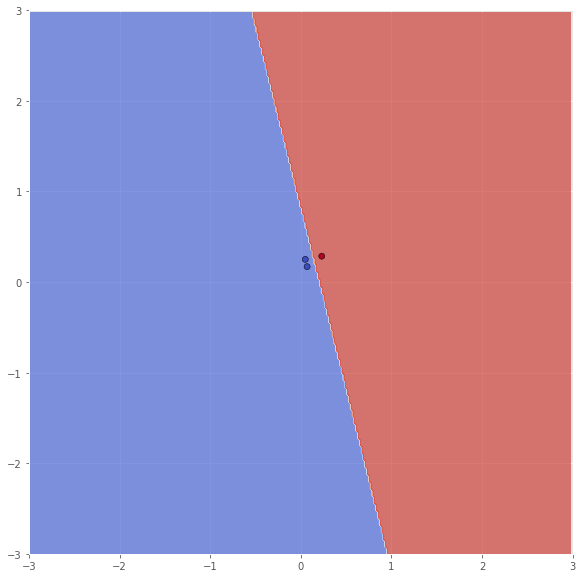
As expected, removing non-support vectors did not change the decision boundary, but let us try removing all except the support vectors.
X_sub = np.array([X[114, :], X[199, :], X[39, :]])
Y_sub = np.array([Y[114], Y[199], Y[39]])
classifier = svm.SVC(C=100.0, kernel='linear')
classifier.fit(X_sub, Y_sub)
xx, yy = make_meshgrid(X_sub, x_range=(-3, 3), y_range=(-3, 3))
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X_sub, Y_sub, xx, yy, Z, x_range=(-3, 3), y_range=(-3, 3))
pretty_print(evaluate(Y_sub, classifier.predict(X_sub)))
Metric name Label 0 Label 1 Average
FN 0.000 0.000 0.000
FP 0.000 0.000 0.000
TN 1.000 2.000 1.500
TP 2.000 1.000 1.500
acc 1.000 1.000 1.000
ppv 1.000 1.000 1.000
tnr 1.000 1.000 1.000
tpr 1.000 1.000 1.000
d)
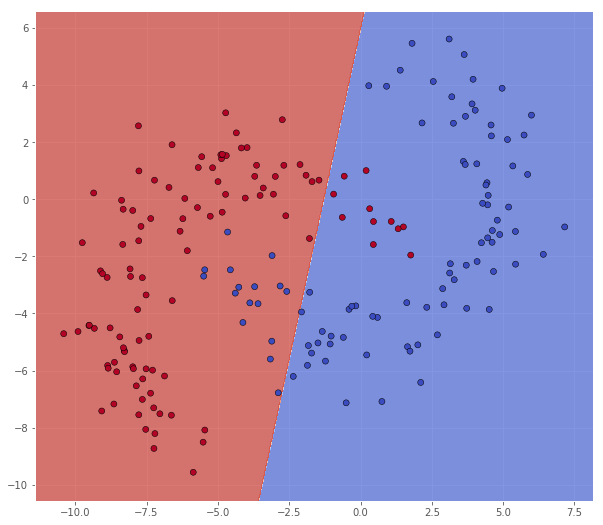
As we see below, the linear svm does a decent job of separating the features, but is of course unable to get a perfect fit on this data.
X = bananadata['A']
Y = np.squeeze(bananadata['a'])
classifier = svm.SVC(C=0.001, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 16.000 11.000 13.500
FP 11.000 16.000 13.500
TN 95.000 78.000 86.500
TP 78.000 95.000 86.500
acc 0.865 0.865 0.865
ppv 0.876 0.856 0.866
tnr 0.896 0.830 0.863
tpr 0.830 0.896 0.863
classifier = svm.SVC(C=0.1, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
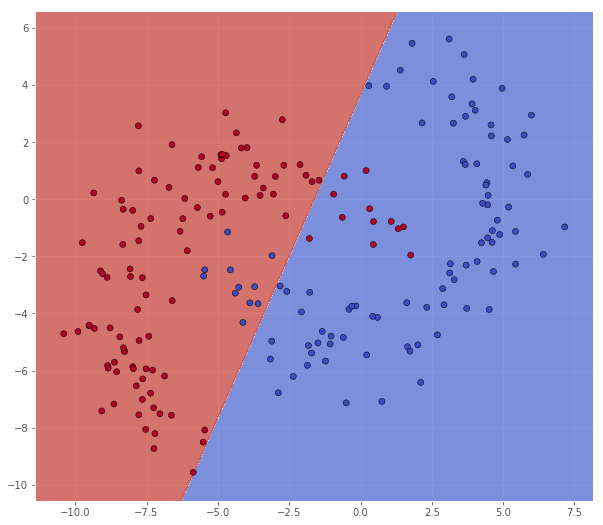
Metric name Label 0 Label 1 Average
FN 11.000 12.000 11.500
FP 12.000 11.000 11.500
TN 94.000 83.000 88.500
TP 83.000 94.000 88.500
acc 0.885 0.885 0.885
ppv 0.874 0.895 0.884
tnr 0.887 0.883 0.885
tpr 0.883 0.887 0.885
classifier = svm.SVC(C=10.0, kernel='linear')
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
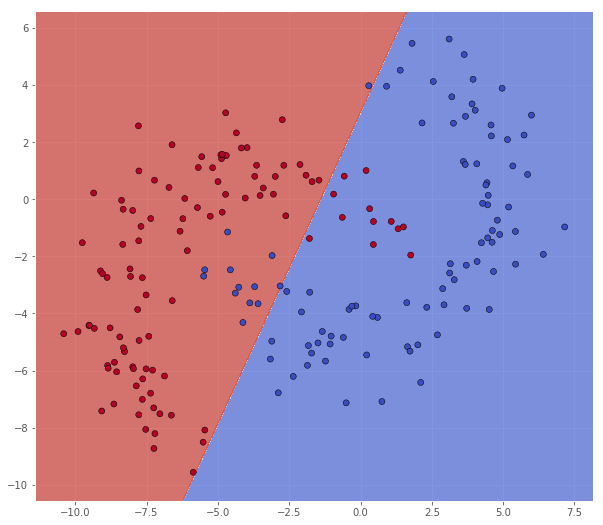
Metric name Label 0 Label 1 Average
FN 13.000 12.000 12.500
FP 12.000 13.000 12.500
TN 94.000 81.000 87.500
TP 81.000 94.000 87.500
acc 0.875 0.875 0.875
ppv 0.871 0.879 0.875
tnr 0.887 0.862 0.874
tpr 0.862 0.887 0.874
e)
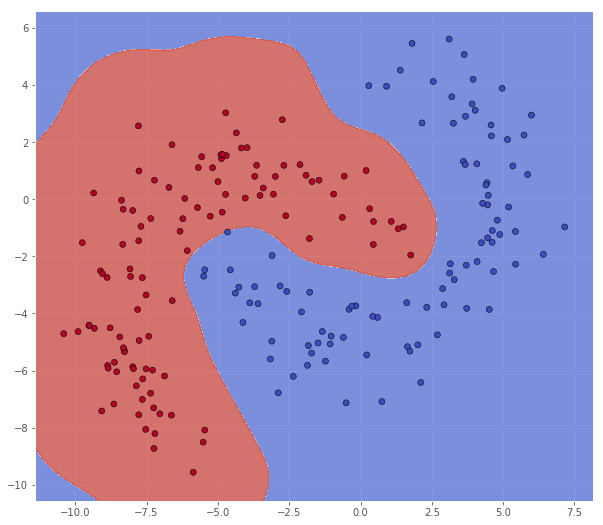
Lets try some different values. The default value seems to be okay.
num_features = 2
classifier = svm.SVC(C=1.0, kernel='rbf', gamma=1/num_features) # This is the default gamma
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 0.000 0.000 0.000
FP 0.000 0.000 0.000
TN 106.000 94.000 100.000
TP 94.000 106.000 100.000
acc 1.000 1.000 1.000
ppv 1.000 1.000 1.000
tnr 1.000 1.000 1.000
tpr 1.000 1.000 1.000
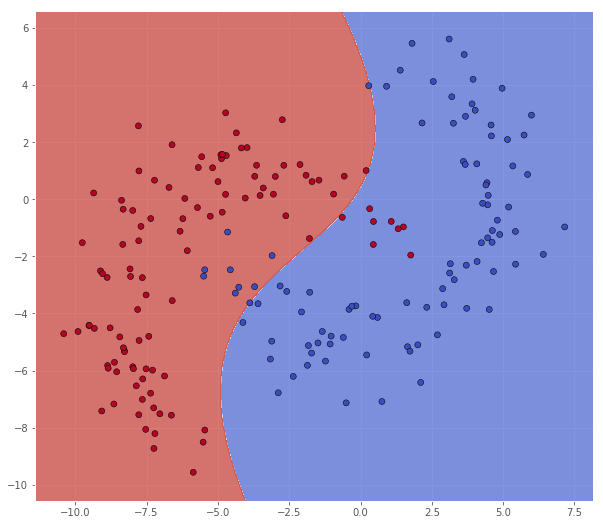
Reducing this seems to underfit the data
classifier = svm.SVC(C=1.0, kernel='rbf', gamma=1e-2)
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 9.000 8.000 8.500
FP 8.000 9.000 8.500
TN 98.000 85.000 91.500
TP 85.000 98.000 91.500
acc 0.915 0.915 0.915
ppv 0.914 0.916 0.915
tnr 0.925 0.904 0.914
tpr 0.904 0.925 0.914
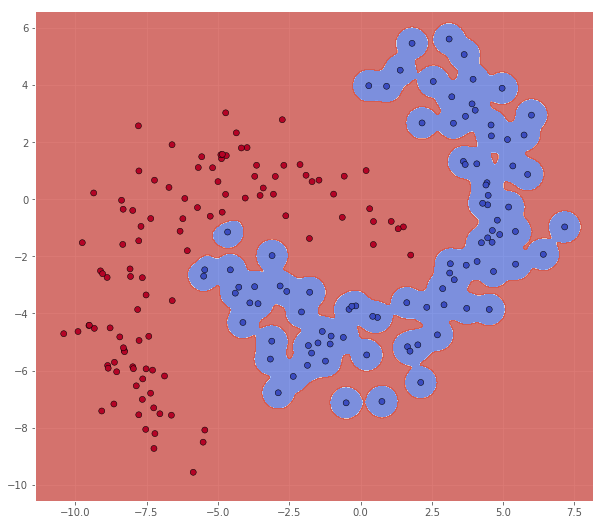
While increasing it seems to overfit
classifier = svm.SVC(C=1.0, kernel='rbf', gamma=10)
classifier.fit(X, Y)
xx, yy = make_meshgrid(X)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X, Y, xx, yy, Z)
pretty_print(evaluate(Y, classifier.predict(X)))
Metric name Label 0 Label 1 Average
FN 0.000 0.000 0.000
FP 0.000 0.000 0.000
TN 106.000 94.000 100.000
TP 94.000 106.000 100.000
acc 1.000 1.000 1.000
ppv 1.000 1.000 1.000
tnr 1.000 1.000 1.000
tpr 1.000 1.000 1.000
f)
Manual grid search with cross-validation
We create a function to do the whole thing.
def manual_grid_search_with_cross_validation(C_arr, gamma_arr):
"""Do a grid search of values in C_arr and gamma_arr using cross-validation.
Note that the sample size of 200 is hard-coded, and the 10-fold cross validation is
carried out with this in mind.
Return a dict of dicts of dicts with evaluation metrics.
metrics_collection[C][gamma] = [metrics_1, metrics_2, ..., metrics_10]
"""
# We partition the data into 10 radom partitions (since we are doing 10-fold cross-validation).
# One way of doing this is to shuffle indices $[0, n-1]$ and then using a different part of indices for each fold.
num_samples = len(Y) # n = 200 in this case
indices = np.arange(0, num_samples)
np.random.shuffle(indices, )
metrics_collection = {}
for C in C_arr:
gamma_metrics = {}
for gamma in gamma_arr:
list_of_metrics = []
for i in range(10):
# Select indices for train and test
start_ind = 20*i
end_ind = start_ind + 20
temp_test_indices = indices[start_ind:end_ind]
test_indices = np.zeros(num_samples, dtype=bool)
test_indices[temp_test_indices] = True
train_indices = (1 - test_indices).astype(bool)
# Partition data
X_train = X[train_indices, :]
Y_train = Y[train_indices]
X_test = X[test_indices, :]
Y_test = Y[test_indices]
# Train
classifier = svm.SVC(C=C, kernel='rbf', gamma=gamma)
classifier.fit(X_train, Y_train)
# Test
Y_test_proposal = classifier.predict(X_test)
# Evaluate
list_of_metrics.append(evaluate(Y_test, Y_test_proposal))
gamma_metrics[gamma] = average_metrics(list_of_metrics)
metrics_collection[C] = gamma_metrics
return metrics_collection
Let us create a printout so that we can make sense of the results
def print_table(metrics_collection, label=None):
"""Print a table of results from each iteration of the grid search.
Either for a given label or the average over labels (default)
"""
header_str = "{0:>11} {1:>11}".format("C", "gamma")
print_header=True
max_vals = {}
for C, gamma_dict in sorted(metrics_collection.items()):
for gamma, avg_met in sorted(gamma_dict.items()):
if print_header:
for key, _ in sorted(avg_met.items()):
header_str += " {0:>11}".format(key)
max_vals[key] = [0.0, 0.0, 0.0]
print(header_str)
print_header = False
result_str = "{0:>11,.4f} {1:>11,.4f}".format(C, gamma)
for key, values in sorted(avg_met.items()):
if label is None:
this_val = np.mean(values)
else:
this_val = values[label]
result_str += " {0:>11,.3f}".format(this_val)
if this_val > max_vals[key][2]:
max_vals[key] = [C, gamma, this_val]
print(result_str)
print("\nMaximum values")
print("{0:<20} {1:>7} {2:>8} {3:>8}".format("Metric name", "value", "C", "gamma"))
for key, val in sorted(max_vals.items()):
print("{0:<20} {1:>7,.3f} {2:>8,.4f} {3:>8,.4f}".format(key, val[2], val[0], val[1]))
def result_matrix(metrics_collection, metric, label):
"""Return a numpy array of values given a metric and a label together with dicts that map
indices to keys and vice versa"""
num_gamma_values = len(next(iter(metrics_collection.values())))
num_C_values = len(metrics_collection.values())
result = np.zeros((num_C_values, num_gamma_values))
C_map = {}
gamma_map = {}
for C_ind, (C, gamma_dict) in enumerate(sorted(metrics_collection.items())):
C_map["key2ind"] = {C_ind: C}
C_map["ind2key"] = {C: C_ind}
for gamma_ind, (gamma, avg_metric) in enumerate(sorted(gamma_dict.items())):
gamma_map["key2ind"] = {gamma_ind: gamma}
gamma_map["ind2key"] = {gamma: gamma_ind}
result[C_ind, gamma_ind] = avg_metric[metric][label]
return result, C_map, gamma_map
def result_array(metrics_collection):
"""Create a 4D matrix of metric results and return it, together with a map to navigate the values in the array.
Args:
metrics_collection: Dictionary of dictionaries of metrics: metrics_collection[C][gamma] = avg_metrics
Returns:
result: A numpy array of shape [num_labels, num_C_values, num_gamma_values, num_metrics]
array_map: A dict of dicts of dicts: array_map[field][mapping][label/key] = key/label
"""
num_labels = len(next(iter(next(iter(next(iter(metrics_collection.values())).values())).values)))
num_metrics = len(next(iter(next(iter(metrics_collection.values())))))
num_gamma_values = len(next(iter(metrics_collection.values())))
num_C_values = len(metrics_collection.values())
result = np.zeros((num_labels, num_C_values, num_gamma_values, num_metrics))
label_map = {}
for label in range(num_labels):
label_map["key2ind"] = {label: label}
label_map["ind2key"] = {label: label}
metric_map = {}
for metric_ind, (metric_key, val) in enumerate(sorted(avg_met.items())):
metric_map["key2ind"] = {metric_key, metric_ind}
metric_map["ind2key"] = {metric_ind, metric_key}
C_gamma_matrix, C_map, gamma_map = result_matrix(metrics_collection, metric_key, label)
result[label, :, :, label] = C_gamma_matrix
array_map = {"label": label_map, "C": C_map, "gamma": gamma_map, "metric": metric_map}
return result, array_map
We are now ready to make some actual experiments.
X = bananadata['A']
Y = np.squeeze(bananadata['a'])
# Note: we do not use the ranges for `C` and `gamma` suggested in the lecture notes.
C_arr = np.power(2.0, np.arange(-5, 10, 2))
gamma_arr = np.power(2.0, np.arange(-5, 6, 2))
metrics_collection = manual_grid_search_with_cross_validation(C_arr, gamma_arr)
print_table(metrics_collection)
C gamma FN FP TN TP acc ppv tnr tpr
0.0312 0.0312 1.250 1.250 8.750 8.750 0.875 0.870 0.871 0.871
0.0312 0.1250 1.700 1.700 8.300 8.300 0.830 0.879 0.839 0.839
0.0312 0.5000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
0.0312 2.0000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
0.0312 8.0000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
0.0312 32.0000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
0.1250 0.0312 0.750 0.750 9.250 9.250 0.925 0.928 0.928 0.928
0.1250 0.1250 0.300 0.300 9.700 9.700 0.970 0.971 0.973 0.973
0.1250 0.5000 0.100 0.100 9.900 9.900 0.990 0.990 0.991 0.991
0.1250 2.0000 4.650 4.650 5.350 5.350 0.535 0.316 0.506 0.506
0.1250 8.0000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
0.1250 32.0000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
0.5000 0.0312 0.450 0.450 9.550 9.550 0.955 0.956 0.954 0.954
0.5000 0.1250 0.100 0.100 9.900 9.900 0.990 0.990 0.991 0.991
0.5000 0.5000 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
0.5000 2.0000 0.350 0.350 9.650 9.650 0.965 0.960 0.972 0.972
0.5000 8.0000 2.900 2.900 7.100 7.100 0.710 0.825 0.700 0.700
0.5000 32.0000 4.700 4.700 5.300 5.300 0.530 0.265 0.500 0.500
2.0000 0.0312 0.150 0.150 9.850 9.850 0.985 0.986 0.986 0.986
2.0000 0.1250 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
2.0000 0.5000 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
2.0000 2.0000 0.100 0.100 9.900 9.900 0.990 0.988 0.992 0.992
2.0000 8.0000 1.400 1.400 8.600 8.600 0.860 0.888 0.874 0.874
2.0000 32.0000 3.150 3.150 6.850 6.850 0.685 0.814 0.669 0.669
8.0000 0.0312 0.100 0.100 9.900 9.900 0.990 0.991 0.991 0.991
8.0000 0.1250 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
8.0000 0.5000 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
8.0000 2.0000 0.100 0.100 9.900 9.900 0.990 0.988 0.992 0.992
8.0000 8.0000 1.400 1.400 8.600 8.600 0.860 0.888 0.874 0.874
8.0000 32.0000 3.150 3.150 6.850 6.850 0.685 0.814 0.669 0.669
32.0000 0.0312 0.100 0.100 9.900 9.900 0.990 0.991 0.988 0.988
32.0000 0.1250 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
32.0000 0.5000 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
32.0000 2.0000 0.100 0.100 9.900 9.900 0.990 0.988 0.992 0.992
32.0000 8.0000 1.400 1.400 8.600 8.600 0.860 0.888 0.874 0.874
32.0000 32.0000 3.150 3.150 6.850 6.850 0.685 0.814 0.669 0.669
128.0000 0.0312 0.000 0.000 10.000 10.000 1.000 1.000 1.000 1.000
128.0000 0.1250 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
128.0000 0.5000 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
128.0000 2.0000 0.100 0.100 9.900 9.900 0.990 0.988 0.992 0.992
128.0000 8.0000 1.400 1.400 8.600 8.600 0.860 0.888 0.874 0.874
128.0000 32.0000 3.150 3.150 6.850 6.850 0.685 0.814 0.669 0.669
512.0000 0.0312 0.100 0.100 9.900 9.900 0.990 0.991 0.990 0.990
512.0000 0.1250 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
512.0000 0.5000 0.050 0.050 9.950 9.950 0.995 0.995 0.995 0.995
512.0000 2.0000 0.100 0.100 9.900 9.900 0.990 0.988 0.992 0.992
512.0000 8.0000 1.400 1.400 8.600 8.600 0.860 0.888 0.874 0.874
512.0000 32.0000 3.150 3.150 6.850 6.850 0.685 0.814 0.669 0.669
Maximum values
Metric name value C gamma
FN 4.700 0.0312 0.5000
FP 4.700 0.0312 0.5000
TN 10.000 128.0000 0.0312
TP 10.000 128.0000 0.0312
acc 1.000 128.0000 0.0312
ppv 1.000 128.0000 0.0312
tnr 1.000 128.0000 0.0312
tpr 1.000 128.0000 0.0312
Note: A pseudo-random number generator is invoked both in the partitioning of the data, and internally in the svm classifier. The analysis may therefore vary from run to run. Ideally, we should have set a random seed in order to reproduce the results.
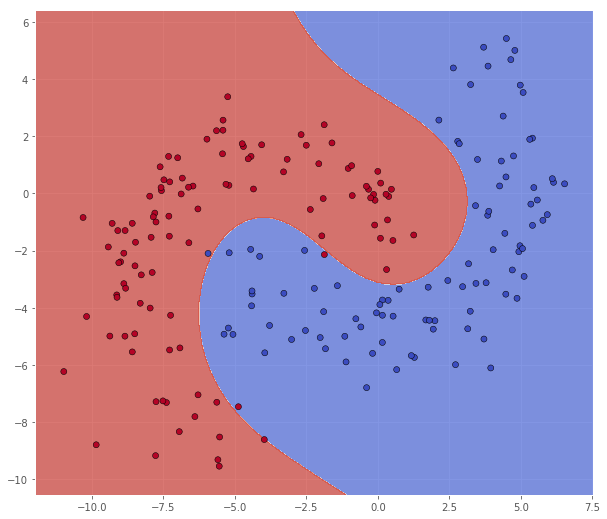
From this run, it looks like $C = 128$ and $\gamma = 0.0312$ is the most promising parameter combination. We will now retrain the model using these values on the entire A dataset, and test it on the B dataset.
X_train = bananadata['A']
Y_train = np.squeeze(bananadata['a'])
classifier = svm.SVC(C=128.0, kernel='rbf', gamma=0.0312)
classifier.fit(X_train, Y_train)
X_test = bananadata['B']
Y_test = np.squeeze(bananadata['b'])
xx, yy = make_meshgrid(X_test)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X_test, Y_test, xx, yy, Z)
pretty_print(evaluate(Y_test, classifier.predict(X_test)))
Metric name Label 0 Label 1 Average
FN 1.000 2.000 1.500
FP 2.000 1.000 1.500
TN 104.000 93.000 98.500
TP 93.000 104.000 98.500
acc 0.985 0.985 0.985
ppv 0.979 0.990 0.985
tnr 0.981 0.989 0.985
tpr 0.989 0.981 0.985
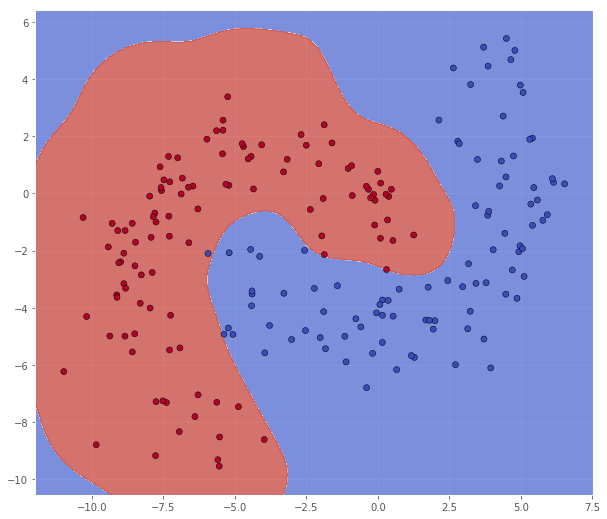
In this case it looks like we achieved quite a good result on the test set. For fun, lets try out with some of the other promising candidates, e.g. $C = 8$ and $\gamma = 0.5$.
classifier = svm.SVC(C=8.0, kernel='rbf', gamma=0.5)
classifier.fit(X_train, Y_train)
X_test = bananadata['B']
Y_test = np.squeeze(bananadata['b'])
xx, yy = make_meshgrid(X_test)
Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
scatter(X_test, Y_test, xx, yy, Z)
pretty_print(evaluate(Y_test, classifier.predict(X_test)))
Metric name Label 0 Label 1 Average
FN 1.000 1.000 1.000
FP 1.000 1.000 1.000
TN 105.000 93.000 99.000
TP 93.000 105.000 99.000
acc 0.990 0.990 0.990
ppv 0.989 0.991 0.990
tnr 0.991 0.989 0.990
tpr 0.989 0.991 0.990
This model actually performs better on the test set. This is something we often encounter in classification, and if we have enough data, it is common to have a hold-out validation set for hyperparameter optimization (in stead of cross-validation). But of course, we cannot have validation sets all the way down, so at some point we have to settle with some model. Inspired by this observation, it is not uncommon to train an ensamble of models (so called ensamble learning) and using some sort of average of the models in the classification.
Parameter grid search with cross-validation using sklearn
For more information, see sklearn’s page on
corss-validation and
grid search. The code below is based on an example found here.
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.svm import SVC
print(__doc__)
parameters = [{'kernel': ['rbf'],
'gamma': gamma_arr,
'C': C_arr}]
metrics = ['accuracy', 'recall_macro']
for metric in metrics:
print("# Tuning hyper-parameters for {}".format(metric))
classifier = GridSearchCV(SVC(), parameters, cv=10, scoring=metric)
classifier.fit(X_train, Y_train)
print("\nBest parameter set found on training set:")
print(classifier.best_params_)
print("\nGrid scores on training set:")
means = classifier.cv_results_['mean_test_score']
stds = classifier.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, classifier.cv_results_['params']):
print("{0:>7,.3f} (+/-{1:>7,.3f}) for {2}".format(mean, std * 2, params))
print("\nDetailed classification report:")
print("\nThe model is trained on the full training set.")
print("The scores are computed on the full test set.")
Y_true, Y_pred = Y_test, classifier.predict(X_test)
print(classification_report(Y_true, Y_pred))
Automatically created module for IPython interactive environment
# Tuning hyper-parameters for accuracy
Best parameter set found on training set:
{'gamma': 0.5, 'kernel': 'rbf', 'C': 0.125}
Grid scores on training set:
0.890 (+/- 0.100) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 0.03125}
0.865 (+/- 0.128) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 0.03125}
0.530 (+/- 0.020) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 0.03125}
0.530 (+/- 0.020) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 0.03125}
0.530 (+/- 0.020) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 0.03125}
0.530 (+/- 0.020) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 0.03125}
0.925 (+/- 0.095) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 0.125}
0.980 (+/- 0.049) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 0.125}
0.995 (+/- 0.030) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 0.125}
0.530 (+/- 0.020) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 0.125}
0.530 (+/- 0.020) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 0.125}
0.530 (+/- 0.020) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 0.125}
0.950 (+/- 0.079) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 0.5}
0.990 (+/- 0.040) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 0.5}
0.990 (+/- 0.039) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 0.5}
0.970 (+/- 0.049) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 0.5}
0.695 (+/- 0.151) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 0.5}
0.530 (+/- 0.020) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 0.5}
0.990 (+/- 0.040) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 2.0}
0.985 (+/- 0.064) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 2.0}
0.990 (+/- 0.039) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 2.0}
0.980 (+/- 0.066) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 2.0}
0.835 (+/- 0.172) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 2.0}
0.690 (+/- 0.166) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 2.0}
0.985 (+/- 0.064) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 8.0}
0.990 (+/- 0.060) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 8.0}
0.990 (+/- 0.039) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 8.0}
0.980 (+/- 0.066) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 8.0}
0.835 (+/- 0.172) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 8.0}
0.690 (+/- 0.166) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 8.0}
0.990 (+/- 0.060) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 32.0}
0.990 (+/- 0.060) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 32.0}
0.990 (+/- 0.039) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 32.0}
0.980 (+/- 0.066) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 32.0}
0.835 (+/- 0.172) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 32.0}
0.690 (+/- 0.166) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 32.0}
0.985 (+/- 0.064) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 128.0}
0.990 (+/- 0.060) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 128.0}
0.990 (+/- 0.039) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 128.0}
0.980 (+/- 0.066) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 128.0}
0.835 (+/- 0.172) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 128.0}
0.690 (+/- 0.166) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 128.0}
0.980 (+/- 0.081) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 512.0}
0.990 (+/- 0.060) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 512.0}
0.990 (+/- 0.039) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 512.0}
0.980 (+/- 0.066) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 512.0}
0.835 (+/- 0.172) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 512.0}
0.690 (+/- 0.166) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 512.0}
Detailed classification report:
The model is trained on the full training set.
The scores are computed on the full test set.
precision recall f1-score support
0 0.98 0.99 0.98 94
1 0.99 0.98 0.99 106
avg / total 0.99 0.98 0.99 200
# Tuning hyper-parameters for recall_macro
Best parameter set found on training set:
{'gamma': 0.5, 'kernel': 'rbf', 'C': 0.125}
Grid scores on training set:
0.888 (+/- 0.100) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 0.03125}
0.856 (+/- 0.136) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 0.03125}
0.500 (+/- 0.000) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 0.03125}
0.500 (+/- 0.000) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 0.03125}
0.500 (+/- 0.000) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 0.03125}
0.500 (+/- 0.000) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 0.03125}
0.924 (+/- 0.099) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 0.125}
0.979 (+/- 0.052) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 0.125}
0.994 (+/- 0.033) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 0.125}
0.500 (+/- 0.000) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 0.125}
0.500 (+/- 0.000) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 0.125}
0.500 (+/- 0.000) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 0.125}
0.949 (+/- 0.084) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 0.5}
0.989 (+/- 0.044) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 0.5}
0.990 (+/- 0.041) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 0.5}
0.969 (+/- 0.052) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 0.5}
0.675 (+/- 0.163) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 0.5}
0.500 (+/- 0.000) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 0.5}
0.989 (+/- 0.044) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 2.0}
0.985 (+/- 0.064) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 2.0}
0.990 (+/- 0.041) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 2.0}
0.980 (+/- 0.065) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 2.0}
0.824 (+/- 0.185) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 2.0}
0.670 (+/- 0.182) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 2.0}
0.984 (+/- 0.066) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 8.0}
0.990 (+/- 0.061) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 8.0}
0.990 (+/- 0.041) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 8.0}
0.980 (+/- 0.065) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 8.0}
0.824 (+/- 0.185) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 8.0}
0.670 (+/- 0.182) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 8.0}
0.990 (+/- 0.061) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 32.0}
0.990 (+/- 0.061) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 32.0}
0.990 (+/- 0.041) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 32.0}
0.980 (+/- 0.065) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 32.0}
0.824 (+/- 0.185) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 32.0}
0.670 (+/- 0.182) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 32.0}
0.985 (+/- 0.066) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 128.0}
0.990 (+/- 0.061) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 128.0}
0.990 (+/- 0.041) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 128.0}
0.980 (+/- 0.065) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 128.0}
0.824 (+/- 0.185) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 128.0}
0.670 (+/- 0.182) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 128.0}
0.979 (+/- 0.084) for {'gamma': 0.03125, 'kernel': 'rbf', 'C': 512.0}
0.990 (+/- 0.061) for {'gamma': 0.125, 'kernel': 'rbf', 'C': 512.0}
0.990 (+/- 0.041) for {'gamma': 0.5, 'kernel': 'rbf', 'C': 512.0}
0.980 (+/- 0.065) for {'gamma': 2.0, 'kernel': 'rbf', 'C': 512.0}
0.824 (+/- 0.185) for {'gamma': 8.0, 'kernel': 'rbf', 'C': 512.0}
0.670 (+/- 0.182) for {'gamma': 32.0, 'kernel': 'rbf', 'C': 512.0}
Detailed classification report:
The model is trained on the full training set.
The scores are computed on the full test set.
precision recall f1-score support
0 0.98 0.99 0.98 94
1 0.99 0.98 0.99 106
avg / total 0.99 0.98 0.99 200
As is evident, me and sklearn did not end up with entirely the same results, but for this data (which is quite easy), the solution space near the solution is quite flat, so that is no surprise. There is also, obviously, the possibility that there are some bugs in my implementation.