Solution proposal - exercise 11
Task 1
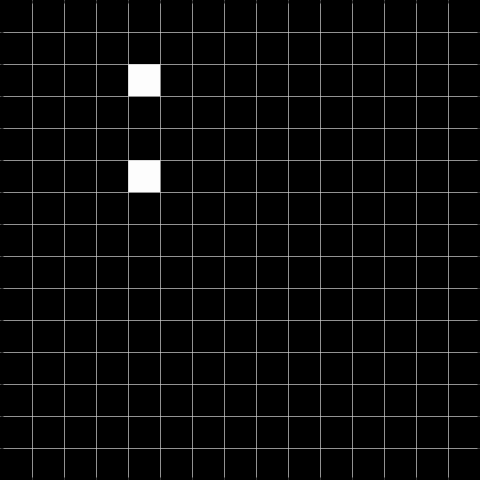
We have several design options for detecting gaps in lines, one such set could be
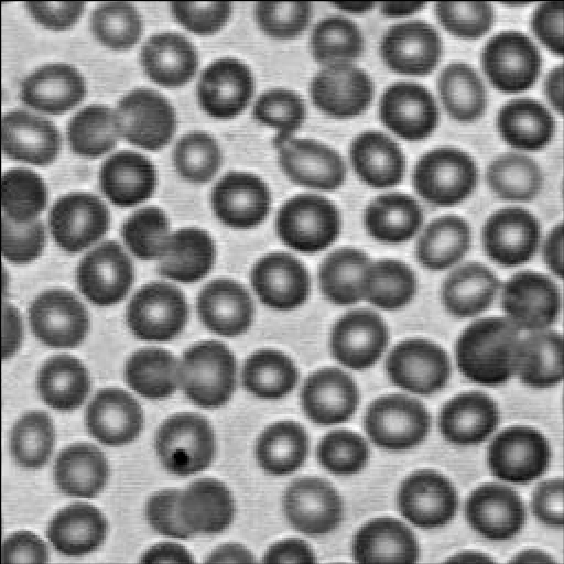
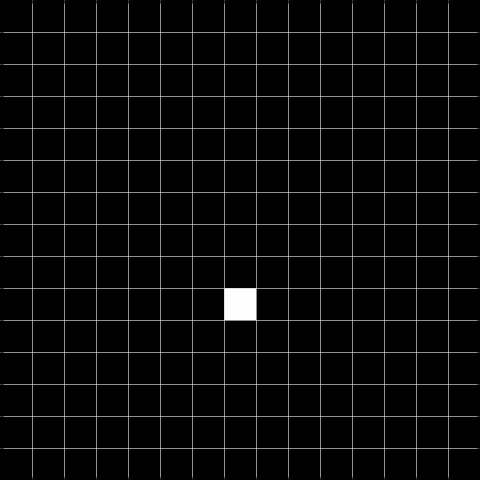
We can use these to detect gaps in horizontal, vertical, diagonal, and antidiagonal lines, respectively. We illustrate this by the dummy image shown in Figure 1.1.

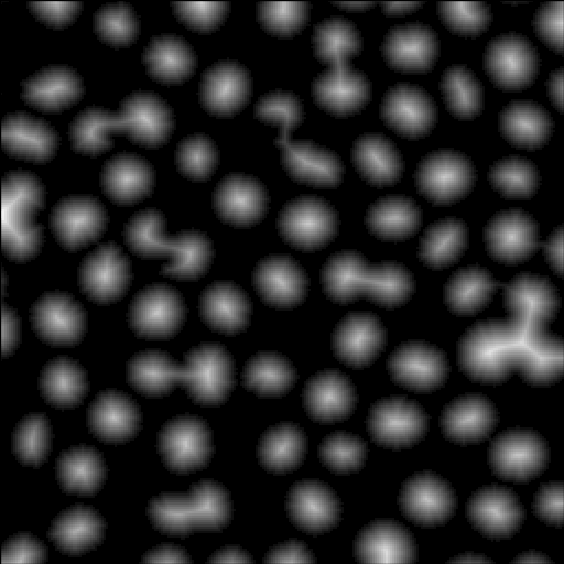
Below, we show the results after convolving the above image with the respective filters. The result to the left is the result of the convolution, and the result to the right is thresholded at 2, and can be used to detect the gaps.

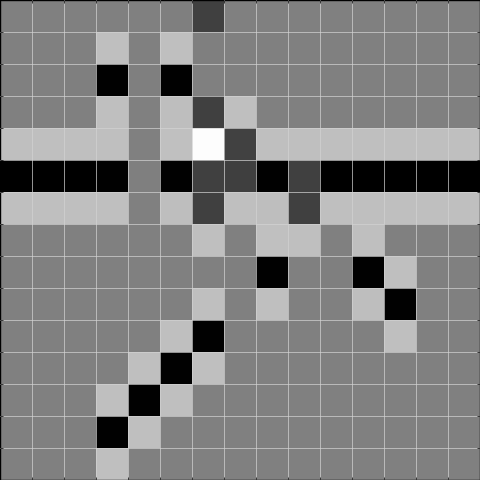
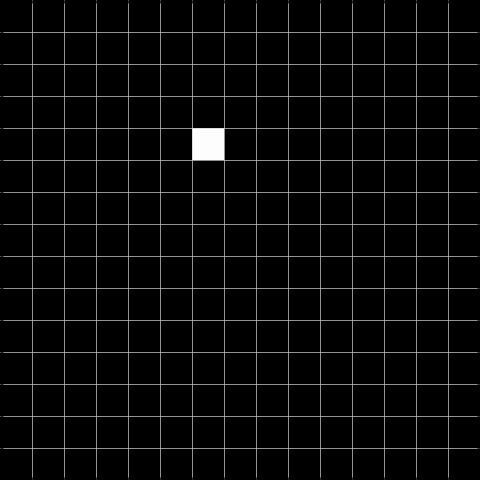
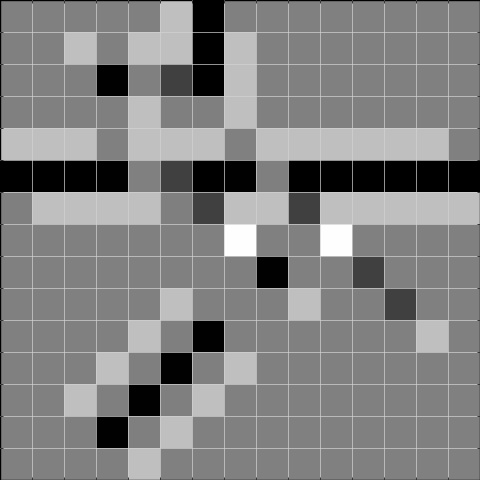
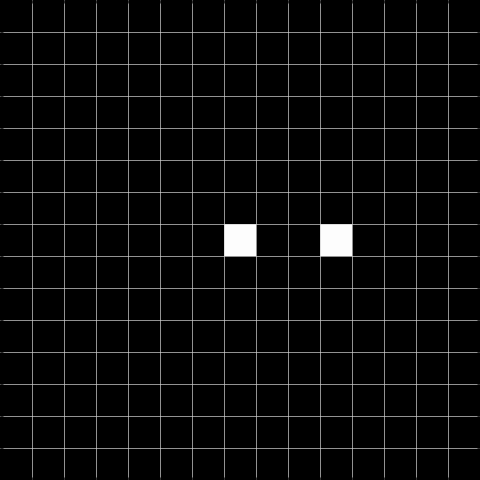
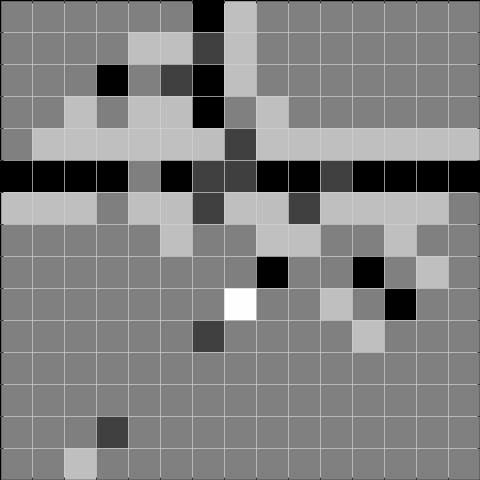
Task 2
The image in problem 10.36 has a number of objects that are brighter than the background. We are given the information that the mean intensity of the backgroud is 60, while the mean intensity of the objects are 170 on a [0 255] scale.
We follow the procedure explained in section 10.4.1 in G&W on region-based segmentation. First, we choose to use foreground-seeds of 170, then use 8-connectivecty to “grow” our regions iteratively if the neighbouring pixel is for example larger than 115.
- Threshold the image at 170 to create a seed image of the foreground.
- For every connected foreground region, add a pixel to this region if:
- The new pixel has gray level above 115
- The new pixel is connected (with 8 connectivity) to the region.
- Continue from 2. until the regions stop growing.
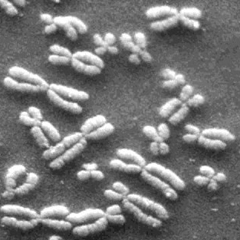
As an example, I have used region growing on the image shown in Figure 2.1 (I could not find the image used in the book).
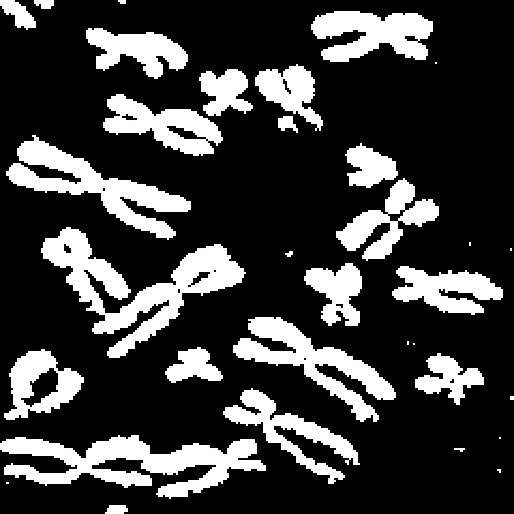
If we try a simple thresholding by Otsu, we get the result shown in Figure 2.2. We see that we also include some bright spots that we do not want. Note that there are probably simpler and/or better methods to segment this particular image, but it gives a simple illustration of the region growing.
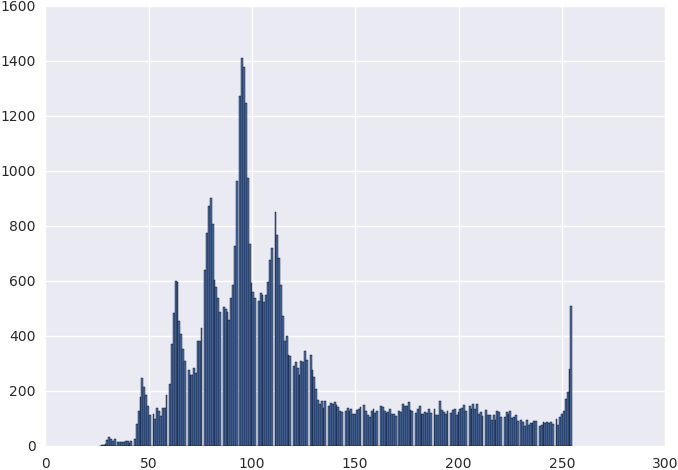
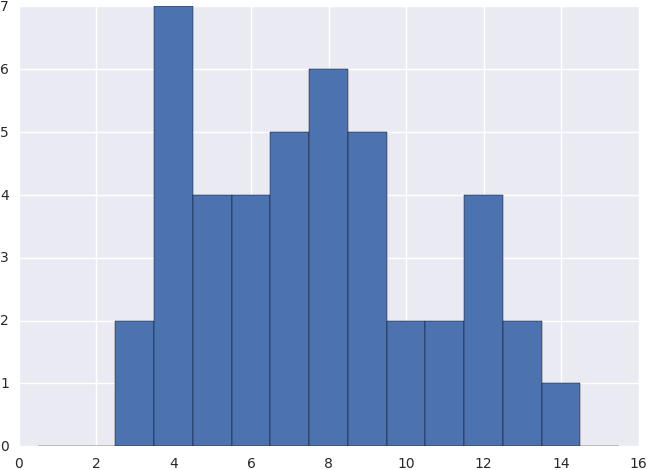
The gray level intensity distribution is shown in Figure 2.2, and from it, we choose the seed level to be 240, and the proposed region threshold to be at 150

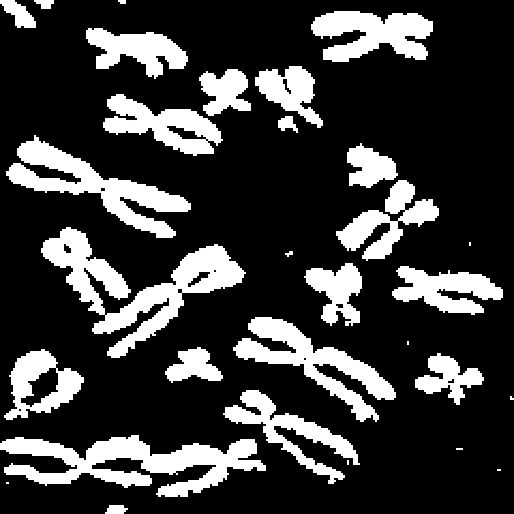
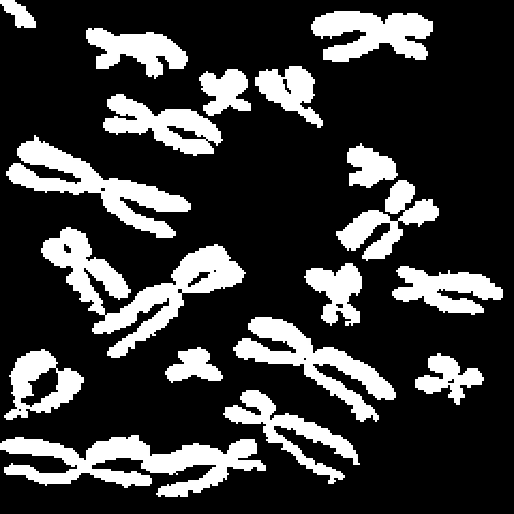
Using region growing of the seed image until convergence yields the final result shown in Figure 2.4.
Task 3
The image we are to segment look like this.

Splitting each quadrant not satisfying the criteria that every value in the region needs to be the same, results in a tree shown in Figure 3.2.

With this, we can merge regions satisfying the criterion. In our case, this will result in a perfect segmentation.
Task 4
The one-dimensional intensity cross section given.
The step by step implementation would look something like this.
- Start with . ()
- Two minimums: and
- Increase to .
- Basin will catch
- Current basins: and
- Increase to .
- Basin will catch .
- New minimum:
- Basin will catch .
- Current basins: , and
- Increase to .
- Nothing happens.
- Increase to .
- New minimum:
- New dam:
- Current basins: , , and
- Current dams:
- Increase to .
- Basin will catch .
- Basin will catch .
- Current basins: , , and
- Current dams:
- Increase to .
- New dam:
- Current basins: , , and
- Current dams: and
- Increase to .
- New dam:
- Current basins: , , and
- Current dams: , and
- Finished! ()
Alternatively with a step prior to where a dam is created at each end of the function, i.e. at and , to prevent the rising water from running off the ends. The remaining steps will be similar, only that the first and last basins won’t include and , respectively.
Task 5




Task 6
First, the grayscale version of the pear image.

This gives quite nice gradients, but some additional things are needed before we can use it for watershed.
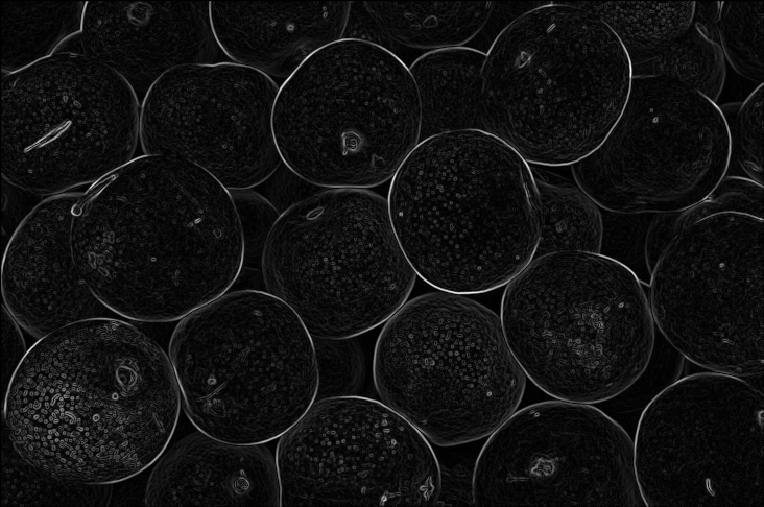
The simple morphological opening follows.

Which can be compared by the opening-by-reconstruction.


The one we are actually going to use is the closing-by-reconstruction of the opening-by-reconstruction.

By using some maximum filters, we can find the regional maxima, and use them as sure foreground.


But first, we clean them a bit.
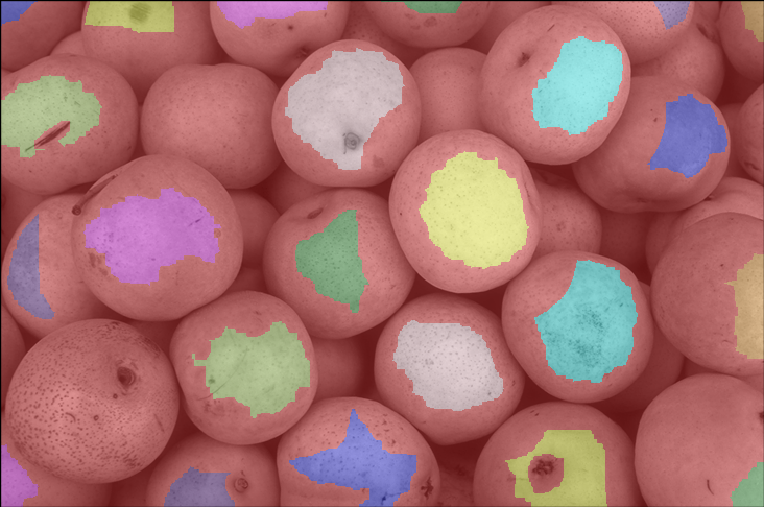
The backgorund in the thresholded image can be used as sure background.

Finally, the watershed results.



Now, if you did compute the SKIZ, you will see that it did not make any significant contribution. The results are as the one above, but with SKIZ.
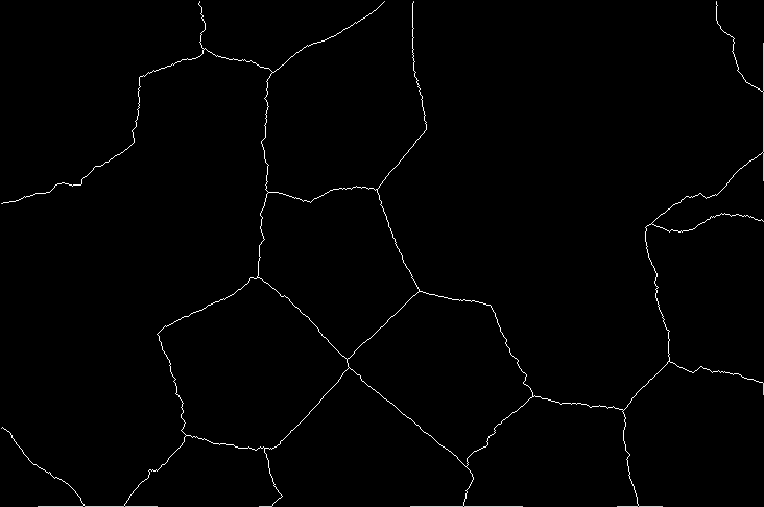



Task 7